|
Escalando una superficie
A veces necesitamos escalar una superficie cuando, por ejemplo, manipulamos la altura o
el radio de la base en un cono o cuando hacemos una simulación de la proyección de un sólido sobre un plano.
En estas y otras situaciones, tenemos uno o varios puntos de arrastre cuyas variables independientes modifican
las otras partes de la superficie.
Para construir una superficie que se pueda escalar, usamos comandos de Mathematica
que soporten expresiones simbólicas, usualmente primitivas (por ejemplo, Plot3D
no las acepta), para construir
la superficie de tal manera
que los polígonos que la conforman estén en función de las variables independientes.
En nuestro primer ejemplo vamos a construir un círculo que se escala al manipular su radio
a través de un punto. En el segundo ejemplo hacemos lo mismo para un cono,
escalándolo al manipular el radio
de la base y su altura, finalmente aplicamos esta idea para simular la
proyección de una superficie sobre el plano YZ
Ejemplo 4
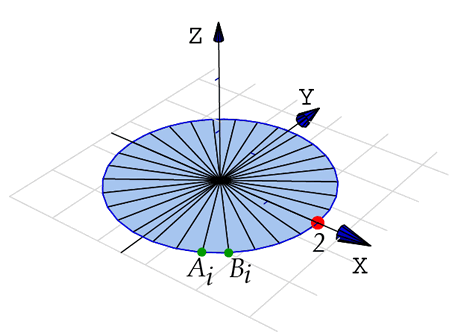
Implementar un círculo
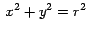 , es decir un círculo de radio variable , es decir un círculo de radio variable 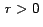 , que se escale con el arrastre de un punto. , que se escale con el arrastre de un punto.
Podemos implementar el círculo con 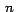 triángulos triángulos
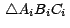 con el vértice con el vértice
 en el centro. Los otros dos puntos tienen un ángulo fijo y dependen del valor del radio.
En efecto, las ecuaciones de los puntos serían en el centro. Los otros dos puntos tienen un ángulo fijo y dependen del valor del radio.
En efecto, las ecuaciones de los puntos serían
aquí
![$\,t_i \,=\, \displaystyle{\frac{i \,2\pi}{n}} \in [0,\, 2\pi], \; i = 0, 1, \cdots, n\,$](img30.gif)
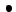 - Para hacer variar
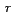 , incluimos en el gráfico el punto de arrastre , incluimos en el gráfico el punto de arrastre Point[{r,0,0}]. Puesto que el arrastre
puede llevar a valores negativos, en vez del radio usamos ra -> Abs[r]
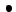 - En la implementación, como pasamos de
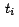 a a 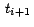 , entonces , entonces 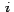 varia de varia de 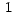 hasta
hasta 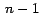 . .
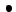 - El cono se construye con 30 puntos. Una versión más 'suave' requiere más puntos, digamos 60 puntos.
Se debe tener en cuenta que, en gráficos más complicados, el peso del archivo '.m' puede hacerse oneroso tanto al descargarlo
como al manipular el gráfico en un navegador.
El código completo es
(*------------------------------- Gráfico ------------------------------*)
independentVariables = {r -> 2};
dependentVariables = {ra -> Abs[r]};
circunferencia =
Line[Table[{0 + ra*Cos[t], 0 + ra*Sin[t], 0} , {t, 0, 2Pi, 0.2}]];
n = 30;
paso = 2Pi/n;
circulo =
Table[Polygon[{ {ra*Cos[i*paso], ra*Sin[i*paso], 0}, {0, 0,0},
{ra*Cos[(i + 1)*paso], ra*Sin[(i + 1)*paso],0},
{ra*Cos[i*paso], ra*Sin[i*paso], 0} }]
, {i, 0, n - 1, 1}];
punto = { AbsolutePointSize[6],
RGBColor[1, 0, 0],
Point[{r, 0, 0}]
};
g = Graphics3D[{Ejes[-02.5, 3, -2.5, 3, -0.1, 3], punto,
EdgeForm[], circulo,
RGBColor[0, 0, 1], circunferencia},
Boxed -> False,
ViewPoint -> {1.761, -2.313, 1.732}];
Show[N[g] //. Join[independentVariables, dependentVariables]];
(*----------------------------- página Web -----------------------------*)
(* Generar la página Web 'ejemplo4.html'. *)
(* El archivo ejemplo4.m es el archivo de coordenadas *)
WriteLiveForm["ejemplo4.m", g, Dir -> "C:\\MisLG3D\\"];
(* Crea la página Web *)
SetDirectory["C:\\MisLG3D\\"];
strm = OpenWrite["ejemplo4.html"];
(* código de la página Web*)
pagina = "<HTML><HEAD></HEAD> <BODY>
<APPLET height=150 width=200 archive=live.jar code=Live.class >
<PARAM NAME=INPUT_FILE VALUE = ejemplo4.m >
<PARAM NAME=INPUT_FILE VALUE = ejemplo4.m >
<PARAM NAME=INDEPENDENT_VARIABLES VALUE='{r->2}'>
<PARAM NAME=DEPENDENT_VARIABLES VALUE='{ra->Abs[r]}'>
</APPLET>
</BODY></HTML>";
(* escribir en el archivo*)
WriteString[strm, pagina];
Close[strm];
|
|
Ejemplo 5
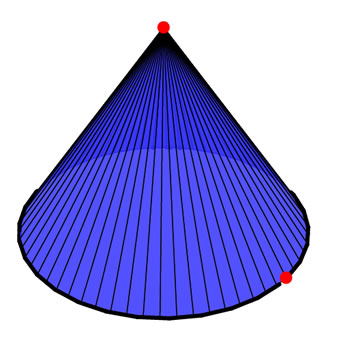
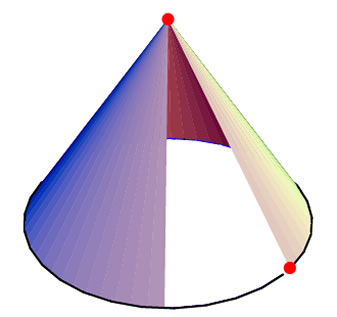
Implementar un cono al que se le pueda manipular la altura y el radio de la base
El código sería similar al del ejemplo anterior. En vez de poner un vértice en
el origen, lo ponemos auna altura adecuada. Vamos a mantener la base circular.
Tendríamos dos variables independientes: la altura y el radio.
|
independentVariables = {r -> 2, h -> 3};
dependentVariables = {ra -> Abs[r], h -> If[h < 0, 0, h]};
circunferencia = Line[
Table[{0 + ra*Cos[t], 0 + ra*Sin[t], 0} , {t, 0, 2Pi, 0.2}]];
n = 60;
paso = 2Pi/n;
circulo =
Table[Polygon[{ {ra*Cos[i*paso], ra*Sin[i*paso], 0}, {0, 0, 0},
{ra*Cos[(i + 1)*paso], ra*Sin[(i + 1)*paso], 0}, {ra*Cos[i*paso], ra*Sin[i*paso], 0} }],
{i, 0, n - 1, 1}];
cva = Line[Table[{0 + 2.01*Cos[t], 0 + 2.01*Sin[t], 0} , {t, 0, 2Pi, 0.2}]];
cono = Table[Polygon[{ {ra*Cos[i*paso], ra*Sin[i*paso], 0}, {0, 0, h},
{ra*Cos[(i +
1)*paso], ra*Sin[(i + 1)*paso], 0},
{ra*Cos[i*paso], ra*Sin[i*paso], 0} }], {i, 0, n - 1, 1}];
puntos = {
AbsolutePointSize[6],
RGBColor[1, 0, 0],
Point[{r, 0, 0}],
Point[{0, 0, h}]
};
g = Graphics3D[{
puntos,
RGBColor[0, 0, 1], circunferencia,
cono,
GrayLevel[0],
AbsoluteThickness[2],
cva},
Boxed -> False, ViewPoint -> {1.761, -2.313,1.732},
PlotRange -> All
];
Show[N[g] //. Join[independentVariables, dependentVariables]];
(*Página Web*)
WriteLiveForm["ejemplo5.m", g, Dir ->
"C:\\MisLG3D\\"];
(* Crea la página Web *)
SetDirectory["C:\\MisLG3D\\"];
strm = OpenWrite["ejemplo5.html"];
(*código de la página Web*)
pagina = "<HTML><HEAD></HEAD> <BODY>
<APPLET height=400 width=400 archive=live.jar code=Live.class >
<PARAM NAME=INPUT_FILE VALUE = ejemplo5.m >
<PARAM NAME=INDEPENDENT_VARIABLES VALUE='{r->2, h->3}'>
<PARAM NAME=DEPENDENT_VARIABLES VALUE='{ra ->Abs[r],h -> If[h<0,0,h]}'>
</APPLET>
</BODY></HTML>";
WriteString[strm, pagina];(*escribe en el archivo*)
Close[strm];
|
|
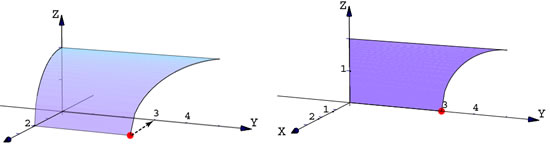
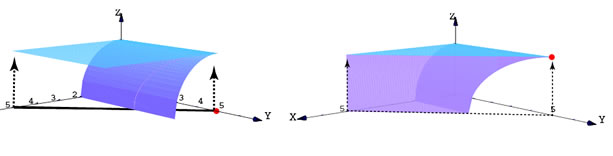
Ejemplo 6 (Proyección perpendicular de una superficie)
Sea 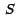 la superficie la superficie 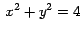 con con
![$\,x \,\in \,[0,2],\,$](img3b.gif) en el primer octante, limitada por el plano en el primer octante, limitada por el plano 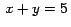 .
Para visualizar la proyección perpendicular de esta superficie sobre el plano YZ, vamos a implementar la superficie
y luego vamos a
declarar a .
Para visualizar la proyección perpendicular de esta superficie sobre el plano YZ, vamos a implementar la superficie
y luego vamos a
declarar a 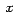 como variable independiente. como variable independiente.
Para proyectar la superficie,
cada primera componente de cada objeto gráfico (excepto los Ejes) la vamos a multiplicar por la variable dependiente ft -> x/2, así conforme 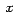 varía de 2 a 0,
la superficie va a sufrir un escalamiento que la va llevar desde su forma original (cuando fx = 1) hasta el
plano YZ (cuando fx = 0). varía de 2 a 0,
la superficie va a sufrir un escalamiento que la va llevar desde su forma original (cuando fx = 1) hasta el
plano YZ (cuando fx = 0).
El código es como sigue
Clear[x, y, z, n];
SetOptions[Arrow3D, HeadScaling3D -> 1, HeadLength3D -> 0.3];
independentVariables = {x -> 2};
dependentVariables = {fx -> x/2};
y[vx_] = 5 - vx;
z[vx_] = Sqrt[4 - vx^2];
vxmin = 0; vxmax = 2;
n = 70;
dvx = (vxmax - vxmin)/n;
Superficie = N[Table[
Polygon[{{ fx*i, 0, z[i]},
{fx* (i + dvx), 0, z[i + dvx]},
{fx* (i + dvx), y[i + dvx], z[i + dvx]},
{ fx*i, y[i], z[i]},
{ fx*i, 0, z[i]}
}],
{i, 0, 2 - dvx, dvx} ]];
contorno = {Line[Table[{fx*i, y[i], z[i]}, {i, 0, 2, 0.05}]],
Line[Table[{fx*i, 0, z[i]}, {i, 0, 2, 0.05}]],
Line[{{fx*2, 0, 0}, {fx*2, 3, 0}}],
Line[{{0, 0, 2}, {0, 5, 2}}]
};
punto = { AbsolutePointSize[6],
RGBColor[1, 0, 0],
Point[{x, 0, 0}],
Point[{x, 3, 0}]
};
g = Graphics3D[{
Ejes[-0.5, 3, -0.5, 6, -0.1, 3], punto,
EdgeForm[],
Superficie,
contorno
},
AmbientLight -> RGBColor[0, 0, 0.356863],
Boxed -> False, ViewPoint -> {2.281, 2.702, 0.572},
PlotRange -> All
];
Show[N[g] //. Join[independentVariables, dependentVariables]];
(* ----------------------Crear la
página Web---------------------*)
WriteLiveForm["ejemplo11.m", g, Dir -> "C:\\MisLG3D\\"];
SetDirectory["C:\\MisLG3D\\"];
strm = OpenWrite["ejemplo11.html"];
(*código de la página Web*)
pagina = "<HTML><HEAD></HEAD> <BODY>
<APPLET height=400 width=400 archive=live.jar code=Live.class >
<PARAM NAME=INPUT_FILE VALUE = ejemplo11.m >
<PARAM NAME=INDEPENDENT_VARIABLES VALUE='{x -> 2}'>
<PARAM NAME=DEPENDENT_VARIABLES VALUE='{x -> If[x<0,0,If[x>2,2,x]], fx->x/
2}'>
</APPLET>
</BODY></HTML>";
WriteString[strm, pagina];(*escribe en el archivo*)
Close[strm];
|
|
Imprimir el valor de una variable
Muchas veces, en el proceso de arrastre de un punto, es conveniente imprimir el valor de una variable o generar
algún evento gráfico. Para imprimir el valor de una variable independiente o dependiente var,
se usa Text[var, a,b,c]. Por ejemplo, para imprimir el valor de una variable 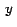 , con dos decimales, se usa , con dos decimales, se usa
independentVariables = {y -> 1};
dependentVariables = {valy -> Round[100*y]/100 };
g = Graphics3D[{Text[valy, {0,y,0}]}]; |
|
Nota: Para poder imprimir el valor de una variable, ésta debe de estar en
la lista de variables dependientes o independientes.
Eventos gráficos
En LG3D, algunos eventos gráficos
se pueden implementar con un If. El uso es muy restringido, solamente se permiten expresiones como
If[ test , listas de primitivas y/o directivas]
Sin embargo, la lista no puede ser una lista invocada con Table[].
Por ejemplo, podemos dibujar una línea con un color distinto dependiendo del valor de la variable
If[variable < 1, {RGBColor[1, 0, 0],Line[{{variable, -1, 0}, {0, 3, 0}}]},
(*sino*) {RGBColor[0, 0, 1],Line[{{variable, -1, 0}, {0, 3, 0}}]}];
También, en vez de Line[Table[{t, 0, 4 - t^2}, {t, 0, 1, 0.2}]]}
(que produce un error de
sintaxis), LG3D reconoce su equivalente
extendido
independentVariables = {y -> 1}
ls = If[y < 3, Line[{{0, 0, 4}, {0.2, 0, 3.96}, {0.4, 0, 3.84},
{0.6, 0, 3.64}, {0.8, 0,3.36}, {1., 0, 3.}}]];
g = Graphics3D[{ls}] |
|
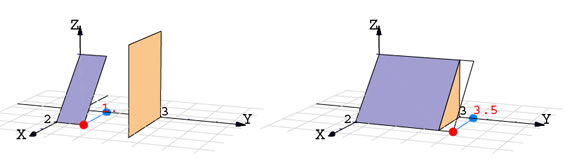
En el siguiente ejemplo hacemos una simulación un poco brusca, del corte de dos planos.
Ejemplo 7
Implementar un gráfico en el que se arrastra el plano 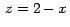 hasta cortar el plano hasta cortar el plano 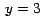 . .
Como el plano esta generado por la recta 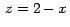 que esta en el plano XZ, la variable de arrastre debe ser que esta en el plano XZ, la variable de arrastre debe ser 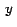 . .
Una idea simple es implementar ambos gráficos con la coordenada 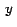 como variable de arrastre,
de tal manera que si como variable de arrastre,
de tal manera que si 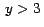 se produzca el corte. se produzca el corte.
El plano 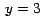 primero es un rectángulo, cuando el arrastre lleva la variable primero es un rectángulo, cuando el arrastre lleva la variable 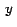 hasta hasta
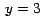 , se cambia a un triángulo. , se cambia a un triángulo.
independentVariables = {y -> 1};
planoY3 =
If[y < 3, {Polygon[{{3, 3, 0}, {0, 3, 0}, {0, 3, 3}, {3, 3, 3}, {3,3, 0}}]},
(*sino*) {Polygon[{{2, 3, 0}, {0, 3, 0}, {0, 3,2}, {2, 3, 0}}]}
]; |
|
El plano 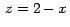 primero es un rectángulo que depende del valor de primero es un rectángulo que depende del valor de 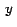 ,
cuando el arrastre lleva la variable ,
cuando el arrastre lleva la variable 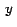 hasta hasta
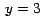 , se fija el rectángulo y se sigue con unas líneas. , se fija el rectángulo y se sigue con unas líneas.
independentVariables = {y -> 1};
planoXZ =
If[y <= 3, {Polygon[{{0, 0, 2}, {2, 0, 0}, {2, y, 0}, {0, y, 2}, {0,0, 2}}]},
(*sino*) {Polygon[{{0, 0, 2}, {2, 0, 0}, {2, 3,0}, {0, 3, 2}, {0, 0, 2}}],
Line[{{0, 3, 2}, {0, y, 2}, {2, y, 0}, {2, 3, 0}}]
}
]; |
|
El código completo es
(*------------------------------- Gráfico ------------------------------*)
(*Opciones para flechas 3D*)
SetOptions[Arrow3D, HeadScaling3D -> 1, HeadLength3D -> 0.3];
independentVariables = {y -> 1};
dependentVariables = {valy -> Round[100*y]/100};
planoXZ =
If[y <= 3, {Polygon[{{0, 0, 2}, {2, 0, 0}, {2, y, 0}, {0, y, 2}, {0,0, 2}}]},
(*sino*) {Polygon[{{0, 0, 2}, {2, 0, 0}, {2, 3,0}, {0, 3, 2}, {0, 0, 2}}],
Line[{{0, 3, 2}, {0, y, 2}, {2, y, 0}, {2, 3, 0}}]
}
];
planoY3 =
If[y < 3, {Polygon[{{3, 3, 0}, {0, 3, 0}, {0, 3, 3}, {3, 3, 3}, {3,3, 0}}]},
(*sino*) {Polygon[{{2, 3, 0}, {0, 3, 0}, {0, 3,2}, {2, 3, 0}}]}
];
punto = { AbsolutePointSize[6],
RGBColor[1, 0, 0],
Point[{2, y, 0}],
Text[ valy, {0, y, 0}, {0, -1}],(*imprime valor de y*)
RGBColor[0, 0.501961, 1],
Point[{0, y, 0}],
Line[{{2, y, 0}, {0, y, 0}}]
};
g = Graphics3D[{Ejes[-02.5, 4, -2.5, 6, -0.1, 3],
punto, planoXZ, planoY3},
Boxed -> False,
ViewPoint -> {3.640, 1.467, 0.793},
PlotRange -> All ];
Show[N[g] //. Join[independentVariables, dependentVariables]];
(*----------------------------- página Web -----------------------------*)
(* Generar la página Web 'ejemplo4.html'. *)
(* El archivo ejemplo6.m es el archivo de coordenadas *)
WriteLiveForm["ejemplo6.m", g, Dir -> "C:\\MisLG3D\\"];
(* Crea la página Web *)
SetDirectory["C:\\MisLG3D\\"];
strm = OpenWrite["ejemplo6.html"];
(* código de la página Web*)
pagina = "<HTML><HEAD></HEAD> <BODY>
<APPLET height=150 width=200 archive=live.jar code=Live.class >
<PARAM NAME=INPUT_FILE VALUE = ejemplo6.m >
<PARAM NAME=INDEPENDENT_VARIABLES VALUE='{y->1}'>
<PARAM NAME=DEPENDENT_VARIABLES VALUE='{valy ->Round[100*y]/100}'>
</APPLET>
</BODY></HTML>";
(* escribir en el archivo*)
WriteString[strm, pagina];
Close[strm];
|
|
Ejemplo 8
Sea 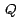 el sólido en el primer octante,
limitado por la superficie el sólido en el primer octante,
limitado por la superficie 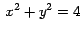 y los planos y los planos 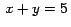 y y 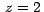 . .
Podemos hacer una pequeña animación, arrastrando un punto, simulando
el corte (un poco brusco) del plano 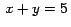 con
la superficie y el otro plano. Para hacer tolerable la superposición inadecuada de superficies, todas las superficies
las construimos con bastantes polígonos. Como estamos usando un 'If', todas las listas de polígonos y líneas se generaron
aparte, con Table[], y luego se pegaron en el código (en el If). con
la superficie y el otro plano. Para hacer tolerable la superposición inadecuada de superficies, todas las superficies
las construimos con bastantes polígonos. Como estamos usando un 'If', todas las listas de polígonos y líneas se generaron
aparte, con Table[], y luego se pegaron en el código (en el If).
Expresiones de Mathematica reconocidas por LG3D
Una expresión tal como
independentVariables = {y -> 1};
dependentVariables = {valy -> Round[100*y]/100};
no nos va a causar un errorr de sintaxis,
en cambio
independentVariables = {y -> 1};
dependentVariables = {valy -> GCD[36,45]};
si nos produce un error.
LG3D reconoce las operaciones básicas: +, -, /, *, >, <, <=, ==, ^, etc. y
muchas otras funciones de Mathematica.
La programación está restringida a
| If[expr1, expr2] |
| If[expr1, expr2,
expr3] |
| If[expr1, expr2,
expr3, expr4] |
| Which[expr1, expr2,
...] |
| Switch[expr1, expr2,
expr3, ...] |
| |
A continuación veremos una lista de expresiones reconocidas por LG3D
| Aritmética |
|
| Plus[expr1, expr2,
...] |
expr1 + expr2 + ... |
| Subtract[expr1, expr2,
...] |
expr1 - expr2 - ... |
| Minus[expr] |
-expr |
| Times[expr1, expr2,
...] |
expr1 expr2 ... |
| Subtract[expr1, expr2] |
expr1 - expr2 |
| Divide[expr1, expr2] |
expr1 / expr2 |
| Power[expr1, expr2,
...] |
expr1 ^ expr2 ^ ... |
| Constantes |
|
| Pi |
3.141592653589793238462643 |
| E |
2.718281828459045235360287 |
| Degree |
0.017453292519943295769237 |
| GoldenRatio |
1.618033988749894848204587 |
| EulerGamma |
0.577215664901532860606512 |
| Catalan |
0.915965594177219015054604 |
| Khinchin |
2.685452001065306445309715 |
| Glaisher |
1.282427129100622636875343 |
I,
Infinity,
Indeterminate,
ComplexInfinity |
in LiveGraphics3D: NaN (not a number)
|
| Funciones |
|
| Abs[expr] |
|
| Sign[expr] |
|
| Round[expr] |
|
| IntegerPart[expr] |
|
| FractionalPart[expr] |
|
| Floor[expr] |
|
| Ceiling[expr] |
|
| Chop[expr] |
|
| Max[expr1, expr2,
...] |
|
| Min[expr1, expr2,
...] |
|
| Re[expr] |
in LiveGraphics3D: expr |
| Im[expr] |
in LiveGraphics3D: 0 |
| Conjugate[expr] |
in LiveGraphics3D: expr |
| Arg[expr] |
in LiveGraphics3D: 0 o Pi |
| Mod[expr1, expr2] |
|
| Quotient[expr1, expr2] |
|
| Random |
|
| Random[] |
|
| SeedRandom[] |
|
| SeedRandom[expr] |
|
| Funciones elementales |
|
| Log[expr] |
|
| Log[expr1, expr2] |
|
| Exp[expr] |
|
| Power[expr1, expr2,
...] |
expr1 ^ expr2 ^ ... |
| Sqrt[expr] |
|
| Sin[expr] |
|
| Cos[expr] |
|
| Tan[expr] |
|
| Csc[expr] |
|
| Sec[expr] |
|
| Cot[expr] |
|
| ArcSin[expr] |
|
| ArcCos[expr] |
|
| ArcTan[expr] |
|
| ArcTan[expr1, expr2] |
|
| ArcCsc[expr] |
|
| ArcSec[expr] |
|
| ArcCot[expr] |
|
| Sinh[expr] |
|
| Cosh[expr] |
|
| Tanh[expr] |
|
| Csch[expr] |
|
| Sech[expr] |
|
| Coth[expr] |
|
| ArcSinh[expr] |
|
| ArcCosh[expr] |
|
| ArcTanh[expr] |
|
| ArcCsch[expr] |
|
| ArcSech[expr] |
|
| ArcCoth[expr] |
|
| Factorial |
|
| Factorial[expr] |
expr! |
| Factorial2[expr] |
expr!! |
| Binomial[expr1, expr2] |
|
| Multinomial[expr1, expr2,
...] |
|
| Pochhammer[expr1, expr2]
|
|
| Gamma[expr] |
|
| Beta[expr1, expr2] |
|
| LogGamma[expr] |
|
| Teoría de números |
|
| Mod[expr1, expr2] |
|
| PowerMod[expr1, expr2,
expr3] |
|
| Quotient[expr1, expr2] |
|
| Hipergeométricas |
|
| Erf[expr] |
|
| Erf[expr1, expr2] |
|
| Erfc[expr] |
|
| Erfi[expr] |
|
| Gamma[expr] |
|
| Beta[expr1, expr2] |
|
| Distribuciones |
|
| DiscreteDelta[expr1, expr2,
...] |
|
| KroneckerDelta[expr1,
expr2, ...] |
|
| UnitStep[expr1, expr2,
...] |
| |
| Programación > Tests |
|
| Equal[expr1, expr2,
...] |
expr1 == expr2 == ... |
| Unequal[expr1, expr2,
...] |
expr1 != expr2 != ... |
| Less[expr1, expr2,
...] |
expr1 < expr2 < ... |
| Greater[expr1, expr2,
...] |
expr1 > expr2 > ... |
| LessEqual[expr1, expr2,
...] |
expr1 <= expr2 <= ... |
| GreaterEqual[expr1, expr2,
...] |
expr1 >= expr2 >= ... |
| NumberQ[expr] |
in LiveGraphics3D: True (1.0) |
| NumericQ[expr] |
in LiveGraphics3D: True (1.0) |
| IntegerQ[expr] |
|
| EvenQ[expr] |
|
| OddQ[expr] |
|
| Positive[expr] |
|
| Negative[expr] |
|
| NonPositive[expr] |
|
| NonNegative[expr] |
|
| TrueQ[expr] |
|
| ValueQ[expr] |
in LiveGraphics3D: True (1.0) |
| Programación > Operadores
lógicos |
|
| Not[expr] |
!expr |
| And[expr1, expr2,
...] |
expr1 && expr2 &&
... |
| Or[expr1, expr2,
...] |
expr1 || expr2 || ... |
| Xor[expr1, expr2,
...] |
|
| Implies[expr1, expr2] |
|
| True |
in LiveGraphics3D: 1.0 |
| False |
in LiveGraphics3D: 0.0 |
| Programación > Control de
evaluación |
|
| Evaluate[expr] |
in LiveGraphics3D: expr |
| Hold[expr] |
in LiveGraphics3D: expr |
| HoldComplete[expr] |
in LiveGraphics3D: expr |
| HoldForm[expr] |
in LiveGraphics3D: expr |
| ReleaseHold[expr] |
in LiveGraphics3D: expr |
| Input and Output |
|
| StandardForm[expr] |
in LiveGraphics3D: expr |
| TraditionalForm[expr] |
in LiveGraphics3D: expr |
| InputForm[expr] |
in LiveGraphics3D: expr |
| OutputForm[expr] |
in LiveGraphics3D: expr |
| DisplayForm[expr] |
in LiveGraphics3D: expr |
| FullForm[expr] |
in LiveGraphics3D: expr |
| NumberForm[expr] |
in LiveGraphics3D: expr |
| ScientificForm[expr] |
in LiveGraphics3D: expr |
| EngineeringForm[expr] |
in LiveGraphics3D: expr |
| PaddedForm[expr] |
in LiveGraphics3D: expr |
|
Revista digital Matemática, Educación e Internet.
Derechos Reservados
|