- ... conexa1.1
- Una región
simplemente conexa
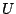 , del plano
, del plano 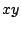 es una región conexa tal
que toda curva cerrada simple en
es una región conexa tal
que toda curva cerrada simple en 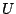 encierra solamente puntos
pertenecientes a
encierra solamente puntos
pertenecientes a 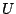 . Intuitivamente es una región que no tiene
hoyos y no consta de partes separadas.
. Intuitivamente es una región que no tiene
hoyos y no consta de partes separadas.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Bernoulli1.2
- Nota
histórica: James Bernoulli propuso esta ecuación para su
solución en 1695. Fue resuelta por su hermano John y en 1696,
Gottfried Leibniz demostró que la ecuación de Bernoulli se
reduce a una ecuación lineal haciendo la sustitución
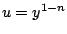
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Clairaut1.3
- Nota histórica:
Alexis Claude Clairaut (1713-1765). Matemático francés.
Estudió este tipo de ecuaciones en el año 1734
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.