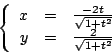|
Ecuación de Clairaut
Suponga que
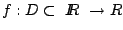 es una función real.
Si es una función real.
Si
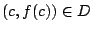 la recta tangente a la gráfica de la
función en este punto está dada por la recta tangente a la gráfica de la
función en este punto está dada por
Observe que esta ecuación es una familia de curvas
uniparamétricas con parámetro 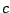 . Entonces podemos encontrar
una ecuación diferencial cuya solución general sea esta
familia de curvas. Si . Entonces podemos encontrar
una ecuación diferencial cuya solución general sea esta
familia de curvas. Si
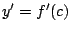 y y
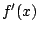 tiene una inversa tiene una inversa 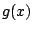 cerca de cerca de 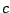 , entonces , entonces
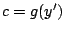 y podemos reescribir la ecuación de la recta
tangente como y podemos reescribir la ecuación de la recta
tangente como
La cual es la ecuación diferencial buscada. A este tipo de
ecuaciones se les conoce como ecuaciones de Clairaut
1.3.
|
|
Definición
[Ecuación de Clairaut]
|
| |
Una ecuación diferencial de primer orden
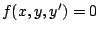 que puede escribirse en la forma
que puede escribirse en la forma
se conoce como ecuación de Clairaut . Donde 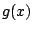 es una función continuamente
diferenciable. es una función continuamente
diferenciable.
|
El interés que presenta este tipo de ecuación se debe al hecho
de que tiene como solución a una familia de rectas. Además,
la envolvente, es decir, la curva cuyas
tangentes están dadas por la familia , también es solución,
en este caso una solución singular,
de la ecuación de Clairaut.
|
|
Teorema[Solución de la ecuación de Clairaut]
|
| |
a ecuación de Clairaut
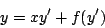 |
(1.18) |
donde 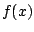 es una función derivable, tiene como solución
general es una función derivable, tiene como solución
general 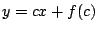 y como solución singular y como solución singular
|
Demostración
Para resolver la ecuación 1.18 hacemos la
sustitución 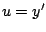 para obtener para obtener
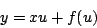 |
(1.19) |
Derivando ambos lados respecto a 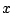
de donde obtenemos que
Surgen dos casos
Caso 1:
Si
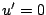 , entonces , entonces 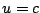 y sustituyendo en la
ecuación 1.19 obtenemos la solución general y sustituyendo en la
ecuación 1.19 obtenemos la solución general
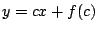 . .
Observe que la solución general se obtiene simplemente
sustituyendo en la ecuación 1.18 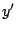 por por
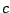 . .
Cso 2:
Si
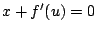 , entonces , entonces
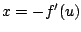 y
sustituyendo en la ecuación 1.19 y
sustituyendo en la ecuación 1.19
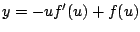 , es decir , es decir
Estas son las ecuaciones paramétricas de una curva donde 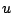 es
el parámetro. Observe que esta solución no es un caso
particular de la solución general, por lo que se trata de una
solución singular. es
el parámetro. Observe que esta solución no es un caso
particular de la solución general, por lo que se trata de una
solución singular.
Ejemplo:
Resuelva la ecuación diferencial
Solución:
La solución general es la familia de rectas
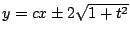 y como y como
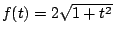 la solución
singular está dada por la solución
singular está dada por
Observe que estas son las ecuaciones paramétricas de una
círculo de radio 2, 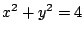 . En la figura
1.2 se muestra la familia de rectas tangentes . En la figura
1.2 se muestra la familia de rectas tangentes
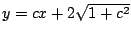 y la envolvente y la envolvente 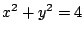 . .
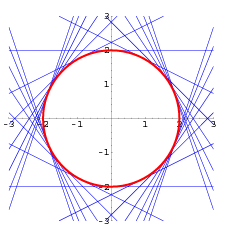
Figura 1.2:
Envolvente 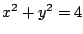 y rectas tangentes y rectas tangentes
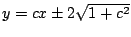 . .
| |
Subsecciones
- Revista virtual
Matemática, Educación e Internet -
ITCR
|