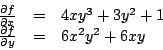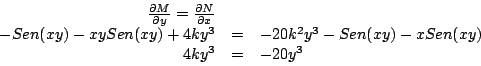|
Ecuaciones diferenciales exactas
Primero debemos retomar algunos conceptos de cálculo vectorial.
Ejemplo
El gradiente de la función
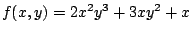 es es
|
|
Definición
[Campo vectorial conservativo]
|
| |
Sea
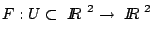 una función vectorial, decimos que una función vectorial, decimos que 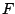 es
un campo vectorial conservativo si existe una función escalar es
un campo vectorial conservativo si existe una función escalar
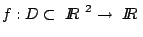 tal que tal que 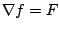 . A la
función escalar . A la
función escalar 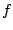 se le llama función potencial. se le llama función potencial.
|
Ejemplo
La función vectorial
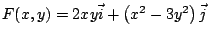 es un campo vectorial conservativo, pues, si es un campo vectorial conservativo, pues, si
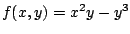 se tiene que se tiene que 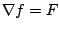 . .
La definición anterior no es muy útil al tratar de verificar
que un campo vectorial es conservativo, pues involucra el hallar
una función potencial. El siguiente teorema nos facilitará
esta tarea.
|
|
Teorema |
| |
Sea
 un campo vectorial definido
sobre una región simplemente conexa1.1 un campo vectorial definido
sobre una región simplemente conexa1.1 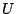 y dado por y dado por
donde 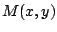 y y 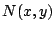 tienen derivadas parciales de primer
orden continuas en tienen derivadas parciales de primer
orden continuas en 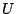 , entonces , entonces 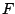 es conservativo sí y sólo
sí es conservativo sí y sólo
sí
|
De paso este teorema nos da la clave para construir la función
potencial, como veremos en el próximo ejemplo.
Ejemplo
El campo vectorial
es conservativo, pues si
tenemos que
Como es conservativo, existe una función escalar 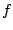 tal que tal que
de donde, como
Derivando con respecto a 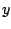 e igualando a la derivada parcial e igualando a la derivada parcial
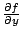
Con lo cual
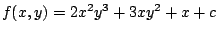 . .
Observación: algunas veces resulta más fácil integrar 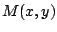 respecto a respecto a 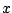 y y
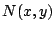 respecto a respecto a 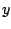 y luego elegimos y luego elegimos 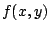 como la suma de ambos, tomando los términos repetidos
una vez. como la suma de ambos, tomando los términos repetidos
una vez.
|
|
Definición
[Ecuación diferencial exacta]
|
| |
Una ecuación diferencial ordinaria de primer orden escrita en la
forma
es exacta si el campo vectorial asociado
es conservativo.
|
|
|
Teorema |
| |
La solución general de la ecuación diferencial exacta
está dada por 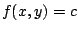 , donde , donde 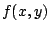 es la función
potencial del campo vectorial es la función
potencial del campo vectorial
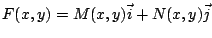 . .
|
Demostración:
Comprobemos que 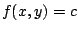 es solución de la ecuación
diferencial. Suponiendo que es solución de la ecuación
diferencial. Suponiendo que 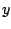 es función de es función de 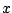 , derivamos
implícitamente , derivamos
implícitamente
Como 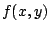 es la función potencial del campo vectorial es la función potencial del campo vectorial
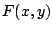 , ,
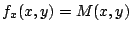 y y
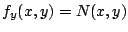 , de donde , de donde
Como se quería.
Ejemplo
La solución general de la ecuación diferencial
es
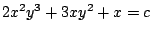 , pues la ecuación diferencial es exacta y
como hemos visto , pues la ecuación diferencial es exacta y
como hemos visto
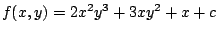 es la
función potencial del campo vectorial es la
función potencial del campo vectorial
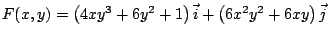 . .
Ejemplo
Determine una función 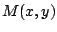 de modo que la ecuación diferencial de modo que la ecuación diferencial
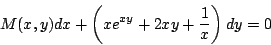 |
(1.1) |
sea exacta.
Para que la ecuación diferencial (1.1) sea exacta debe cumplirse que
Y al integrar respecto a 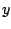 , obtenemos que , obtenemos que
Observación: en realidad obtenemos toda una familia de funciones 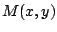 , debido a la constante de
integración , debido a la constante de
integración 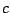 , como queremos sólo una función , como queremos sólo una función 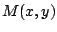 podemos tomar podemos tomar 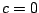 . .
Ejemplo
Determine el valor o valores de 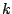 de forma que la ecuación diferencial de forma que la ecuación diferencial
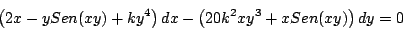 |
(1.2) |
Para que la ecuación diferencial (1.2) sea exacta debe satisfacer
de donde obtenemos que
Subsecciones
Revista digital Matemática, Educación e Internet.
|