|
| 1 2 3 4 5 6 |
Apartados c) y e):
|
xk |
f(xk) = ln(xk) |
Método de Newton P3(2) f(2) –P3(2) |
Método de Lagrange P3(2) f(2) –P3(2) |
|
1 |
0 |
0.628784 0.06436318 |
0.6287687 0.0643785 |
|
6 |
1.7917595 |
||
|
4 |
1.3862944 |
||
|
5 |
1.6094379 |
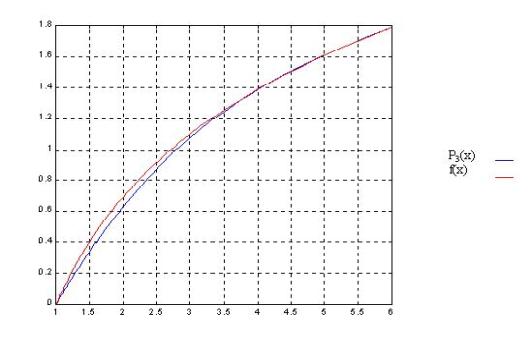
Apartado d): Estimación del error del polinomio de interpolación de Newton de segundo orden
R2 (2 ) = (2-1)(2-4)(2-6) f(1 4 6 5) = 8 * 0.00786553 = 0.06292424
Cota del error del polinomio de interpolación de Newton de tercer orden
R3(x)
=
con
entre x0 y xi,,
f (4) (x) = -6 x
-4
R3
(2) = (2-1) (2-4) (2-5) (2-6)( -6
-4) / 24 = 6
-4, para 1<
<6, obtenemos
6*5 -4
E(2)
6*4 -4
, es decir,
0.0096
E(2)
0.023475
Apartado e): Cota del error del polinomio de interpolación de Lagrange de tercer orden
R3(x)
=
con
entre x0 y xi
,
f
(4) (x) = -6 x -4
R3
(2) = (2-1) (2-4) (2-5) (2-6)( -6
-4) / 24 = 6
-4, para 1<
<6, obtenemos
6*5 -4
E(2)
6*4 -4
, es decir, 0.0096
E(2)
0.023475
Conclusiones a las que arribaron los alumnos luego de
realizar esta actividad:
1. En el apartado a) se usan dos interpolaciones lineales para aproximar ln 2. El intervalo más pequeño proporciona una mejor aproximación.
Los resultados obtenidos con el polinomio de interpolación de Lagrange están en estrecha concordancia con los obtenidos usando la interpolación polinomial de Newton con diferencias divididas.
2. La interpolación cuadrática realizada en el apartado b) mejora la interpolación comparada con los resultados obtenidos al usar una línea recta.
Los resultados obtenidos con el polinomio de interpolación de Lagrange están en estrecha concordancia con los obtenidos usando la interpolación polinomial de Newton con diferencias divididas.
3. La interpolación cúbica realizada en el apartado c) mejora la interpolación comparada con los resultados obtenidos al usar una línea recta o una parábola.
Los resultados obtenidos con el polinomio de interpolación de Lagrange están en estrecha concordancia con los obtenidos usando la interpolación polinomial de Newton con diferencias divididas.
4. La estimación del error obtenido en el apartado d) es del mismo orden que el error verdadero obtenido en el apartado b). Las cotas del error obtenidas en d) y en e) coinciden, como era de esperarse.
5. Si no se conoce la función, la fórmula de Newton es mejor porque permite ir analizando el polinomio de interpolación a partir de las diferencias divididas de orden superior obtenidas. Además, a partir de las mismas se puede obtener una estimación del error cometido en la aproximación.