| 1 2 3 4 5 6 |
Actividad 3
El valor promedio de una corriente eléctrica oscilante durante un período puede ser cero. Por ejemplo, supóngase que la corriente se describe mediante una senoidal simple
i(t) = sen (2p t/T)
en donde T es el período. El valor promedio de esta función se puede determinar mediante la siguiente ecuación
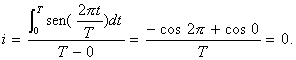
A pesar de que la corriente es igual a cero, esta corriente es capaz de realizar trabajo y generar calor. Por lo tanto, los ingenieros eléctricos, a menudo, caracterizan esta corriente mediante
IRMS
=
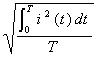 (1)
(1)
en donde IRMS se conoce como corriente RMS (raíz cuadrada media). Para evitar este resultado nulo, la corriente se eleva al cuadrado antes de calcular el promedio.
En este caso, supóngase que la corriente en un circuito es de
i(t)
= 10 e-t/T.![]() para 0
para 0
![]() t
t
![]() T/2
T/2
(2)
i(t)=
0
para T/2
![]() t
t
![]() T
T
Determínese la corriente RMS ajustando un polinomio de segundo grado que coincida con i2(t) exactamente en t=0, T/4, T/2. Luego, intégrese este polinomio analíticamente y calcúlese la corriente RMS en el intervalo de 0 a T usando la ecuación (1). Supóngase que T =1s. Grafíquese el polinomio de segundo orden y la corriente verdadera. Escríbanse las conclusiones a las que se arribaron.
Observación. Este resultado se podrá comparar más adelante cuando veamos integración numérica. Se usarán varias técnicas de integración numérica (utilizando el polinomio de interpolación) para llevar a cabo esos mismos cálculos.
Resultados
obtenidos por los alumnos:
|
Datos
obtenidos a partir de la ecuación (2) |
||
|
t |
i(t) |
i2(t) |
|
0 |
0.000000000 |
0.00000000 |
|
1/4 |
7.788007831 |
60.65306598
|
|
1/2 |
0.000000000 |
0.00000000 |
Ajustando un polinomio de Newton de segundo orden, se obtiene
i2(t)
= 242.612
264 t - 970.449056 t(t- 1/4)
![]()
IRMS = 4.496408418.
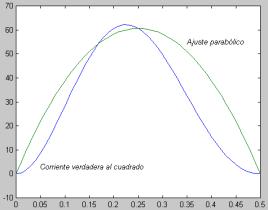
Gráfica de la corriente verdadera junto con la parábola que se usa como aproximación.
Conclusiones a las que arribaron los alumnos luego de
desarrollar esta actividad:
Aproximamos una función complicada por un simple polinomio de interpolación.