| 1 2 3 4 5 6 |
Actividad 2
El mástil de un barco tiene un área transversal de 0.876 pulg2 y se construye de una aleación de aluminio experimental. Se llevan a cabo pruebas para definir la relación entre esfuerzo (fuerza por área) aplicada al material y deformación (deflexión por unidad de longitud). Los resultados de estas pruebas se resumen en el Cuadro 1.
Cuadro
1. Datos de esfuerzo-deformación ordenados de tal manera que los puntos usados
en la interpolación estén siempre más cercanos al esfuerzo de 7350 lb/pulg2.
|
Número
de puntos |
Esfuerzo
lb/pulg2 |
Deformación
pies/pie |
|
1
2
3
4
5
6 |
7200
7500
8000
5200
10000
1800 |
0.0020
0.0045
0.0060
0.0013
0.0085
0.0005 |
Es necesario calcular el cambio de longitud del mástil debido a la deformación causada por la fuerza del viento. La compresión causada por el aire se puede calcular usando la relación
Esfuerzo
=
![]() .
.
En este caso, se tiene una fuerza del viento de 6440.6 libras y el esfuerzo se calcula mediante
Esfuerzo
=
![]() 7350 lb/pulg2.
7350 lb/pulg2.
Este esfuerzo puede ser usado para calcular la deformación, la cual a su vez se puede sustituir en la ley de Hooke y calcular el cambio de la longitud del mástil
Dl = (deformación )(longitud),
en donde la longitud es la altura del mástil. Por lo tanto, el problema se reduce a la determinación de valores de la deformación de los datos del Cuadro 1. Ya que no se dispone de ningún punto para un valor de esfuerzo dado de 7350, el problema necesitará de algún ajuste de curvas.
Úsese interpolación polinomial de Newton de orden 0 al 5 para calcular la deformación a un esfuerzo de 7350 lb/pulg2.
Grafíquese el polinomio de quinto orden que ajusta los datos del Cuadro 1. Escríbanse las conclusiones a las que se arribaron.
Observación. Aunque la curva pase muy bien a través de los puntos en la vecindad del esfuerzo de 7350 lb/pulg2, se observará que ésta oscila en otras partes del rango de datos.
Esto es, debido a que los tres datos se encuentran muy cercanos del valor de 7350 lb/pulg2 la interpolación no debe variar significativamente en este punto, como es de esperarse. Sin embargo, si se requieren aproximaciones de otras fuerzas las oscilaciones de los polinomios pueden llevar a resultados inexactos. Estos resultados ilustran que la interpolación con polinomios de grado superior está mal condicionada para datos inciertos o con "ruido" del tipo a los de este problema. La regresión, como veremos más adelante, proporciona una alternativa que, en general, es más apropiada para estas situaciones.
Resultados obtenidos por los alumnos:
Resultados
del polinomio de interpolación de Newton para predecir una deformación
correspondiente a un esfuerzo de
7350 lb/pulg2 en base a la información del Cuadro 1.
|
Orden
del polinomio (n) |
Coeficientes
de n-ésimo orden |
Deformación
(con esfuerzo = 7350 lb/pulg2 ) |
|
0
1
2
3
4
5 |
2
x 10-3
8.33
x 10-6
-6.67
x 10-9
-3.62
x 10-12
1.198
x 10-15
2.292
x 10-19 |
2
x 10-3
3.27
x 10-3
3.42
x 10-3
3.36
x 10-3
3.401
x 10-3
3.38
x 10-3 |
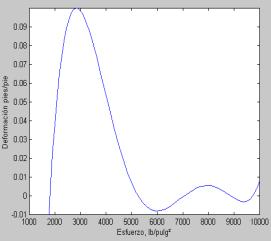
Gráfica
del polinomio de interpolación de
Newton de quinto orden que ajusta perfectamente los datos del Cuadro 1.
Conclusiones a las que arribaron los alumnos luego de
realizar esta actividad:
1. Los datos en el Cuadro 1 fueron ordenados de tal manera que la interpolación siempre use información que se encuentre más cercana a los puntos incógnitas.
2. Todos los polinomios, excepto el de orden cero, llevan a resultados que casi coinciden.
3. Una deformación de aproximadamente 3.4 x 10-3 pies/pie es una aproximación razonable.