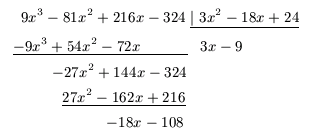

Supongamos que se van a buscar los ceros de un polinomio f (x), lo primero que se tiene que buscar al utilizar el Teorema de Sturm es un sistema de polinomios especial para poder evaluar en él, veamos cómo calcular este sistema.
El primer polinomio es el propio f (x); el segundo polinomio es f'(x), es decir, la derivada del polinomio f (x), a este polinomio lo vamos a denotar f1(x); para el tercer polinomio se debe realizar la división de f (x) entre f1(x), el residuo que se obtiene con signo contrario será f2(x); este proceso se continúa, es decir, f3(x) será el residuo con signo contrario de la división de f1(x) entre f2(x); el proceso acaba cuando se obtiene una constante.
Si los cálculos se van hacer a mano, existe una forma de hacer que no aparezcan fracciones en la división, haciéndola más sencilla, si el dividendo es
P(x) = anxn + ... + a0 y el divisor es
Q(x) = bmxm + ... + b0, entonces multiplique P(x) por
bmn - m + 1. Si la división la hará la computadora, no hace falta multiplicar el dividendo ya que esto no afecta el resultado del Teorema de Sturm y a la computadora le da lo mismo hacer los cálculo con fracciones o sin ellas.
Veamos un ejemplo,
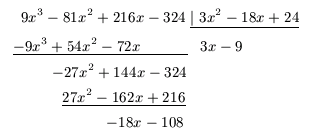
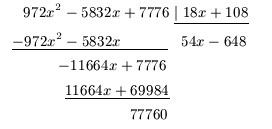
Por lo tanto f3(x) = - 77760


Revista Matemáticas, Educación
e Internetâ
Derechos Reservados