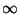 y +
y + 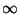 , también evaluamos en x = 0 para verificar cuántos ceros positivos y cuántos negativos hay, veamos
, también evaluamos en x = 0 para verificar cuántos ceros positivos y cuántos negativos hay, veamos

Observe que el teorema pide que la ecuación no tenga raíces múltiples, en este escrito no tomaremos muy en cuenta esta limitación, primero porque la probabilidad que una persona evalúe un polinomio así es bajo, además que el teorema funciona bien para muchos polinomios con raíces múltiples, es decir, son muy pocos los polinomios de raíces múltiples que fallan.
Ahora ilustremos el teorema con un ejemplo.
Ya conocemos el sistema de Sturm para este polinomio (se calculó en la sección anterior)
f (x) = x3 - 9x2 + 24x - 36
f1(x) = 3x2 - 18x + 24
f2(x) = 18x + 108
f3(x) = - 77760
Lo primero para aislar los ceros es revisar cuántos hay en total, así que se evalúa el sistema en - 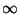 y +
y + 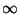 , también evaluamos en x = 0 para verificar cuántos ceros positivos y cuántos negativos hay, veamos
, también evaluamos en x = 0 para verificar cuántos ceros positivos y cuántos negativos hay, veamos
| Signos | - 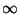 |
0 | + 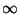 |
| f (x) | - | - | + |
| f1(x) | + | + | + |
| f2(x) | - | + | + |
| f3(x) | - | - | - |
| Cambios | 2 | 2 | 1 |
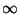 hay 2 cambios de signo y en +
hay 2 cambios de signo y en + 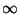 solo hay uno entonces de -
solo hay uno entonces de - 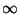 a +
a + 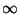 hay 2 - 1 = 1 ceros, es decir, el polinomio solo tiene un cero en
I R.
hay 2 - 1 = 1 ceros, es decir, el polinomio solo tiene un cero en
I R.
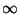 a 0 no hay ceros pues ambos tienen igual número de cambios de signo, así que el cero se encuentra de 0 a +
a 0 no hay ceros pues ambos tienen igual número de cambios de signo, así que el cero se encuentra de 0 a + 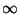 pues al realizar la resta de cambios de signo se obtiene 2 - 1 = 1. Ahora podemos ir evaluando de uno en uno empezando desde 0 hasta encontrar en qué intervalo se encuentra.
pues al realizar la resta de cambios de signo se obtiene 2 - 1 = 1. Ahora podemos ir evaluando de uno en uno empezando desde 0 hasta encontrar en qué intervalo se encuentra.
| Signos | 1 | 2 | 3 | 4 | 5 | 6 |
| f (x) | - | - | - | - | - | 0 |
| f1(x) | + | 0 | - | 0 | + | + |
| f2(x) | + | + | + | + | + | + |
| f3(x) | - | - | - | - | - | - |
| Cambios | 2 | 2 | 2 | 2 | 2 | 1 |
Revista Matemáticas, Educación
e Internetâ
Derechos Reservados