![$\displaystyle \sqrt[k]{\frac{G}{a_n}}$](images/img14.gif)

Hay varias formas para encontrar la cota superior de un polinomio, aquí presentaremos dos, no se puede decir que una sea mejor que la otra, simplemente un método da la mejor cota para algunas funciones y el otro método es el mejor para otras.
Se debe notar que estos teoremas son para encontrar la cota superior, sin embargo, para encontrar la cota inferior simplemente debemos aplicar estos teoremas al polinomio f (- x) (esta evaluación invierte el polinomio, convirtiendo los ceros positivos en negativos y viceversa), veamos estos dos teoremas
![$\displaystyle \sqrt[k]{\frac{G}{a_n}}$](images/img14.gif)
Una condición del teorema es que an > 0, es decir, que el coeficiente del primer término debe ser positivo, pero si esto no sucede, tan solo se debe multiplicar el polinomio por -1 ya que - f (x) = 0 tiene los mismos ceros que f (x) = 0.
![$\displaystyle \sqrt[1]{\frac{36}{1}}$](images/img15.gif) =1+36=37.
=1+36=37.
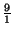 =9,
c2=
=9,
c2=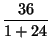 =1.44. Como se debe tomar el mayor aumentado en uno, la cota es 9 + 1 = 10.
=1.44. Como se debe tomar el mayor aumentado en uno, la cota es 9 + 1 = 10.
Observe que una vez que se tiene el intervalo en donde se encuentra el cero, se puede ir partiendo ese intervalo a la mitad y así ir aislando cada solución. Por ejemplo, se puede verificar con el teorema de Sturm en x = 0, 5, 10, así se eliminan 5 valores de una vez y nos quedaría el intervalo ]5, 10[, luego se repite el proceso varias veces hasta tener bien aislado el cero (se puede ver que este proceso se asemeja mucho al proceso de bisección).
Veamos ahora un ejemplo completo que haga uso de todos los teoremas.
La cota superior es
1+![$\displaystyle \sqrt[3]{\frac{7}{1}}$](images/img18.gif)
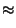 3
3
Para la cota inferior usamos el polinomio
- f (- x) = x3 - 4x2 + 7. La cota es
1+![$\displaystyle \sqrt[1]{\frac{4}{1}}$](images/img20.gif) = 5.
= 5.
Por lo tanto los ceros se encuentran en el intervalo ]-5, 3[.
Con el segundo teorema se obtiene
Para la cota superior, como solo hay un coeficiente negativo, la cota es
1+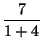 =2.4. Tomemos 3 como cota superior.
=2.4. Tomemos 3 como cota superior.
Para la inferior, se utiliza el polinomio
- f (- x) = x3 - 4x2 + 7 y se obtiene como cota
1+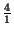 =5. Por lo que la cota inferior es -5.
=5. Por lo que la cota inferior es -5.
Así, los ceros están en el intervalo ]-5, 3[, este intervalo es igual al que se obtuvo anteriormente, por lo que es el que se utilizará al aplicar el teorema de Sturm.
El sistema de Sturm ya lo habíamos calculado anteriormente y se obtuvo que
f (x) = x3 + 4x2 - 7
f1(x) = 3x2 + 8x
f2(x) = 32x + 63
f3(x) = 4221
Primero calculamos el sistema en -  , 0 y +
, 0 y +  para ver cuántos ceros hay en total y cuántos son positivos y cuántos negativos.
para ver cuántos ceros hay en total y cuántos son positivos y cuántos negativos.
| Signos | -  |
0 | +  |
| f (x) | - | - | + |
| f1(x) | + | 0 | + |
| f2(x) | - | + | + |
| f3(x) | + | + | + |
| Cambios | 3 | 1 | 0 |
| Signos | f (x) | f1(x) | f2(x) | f3(x) | Cambios |
| x = 1 | - | + | + | + | 1 |
Ahora aislemos las negativas
| Signos | f (x) | f1(x) | f2(x) | f3(x) | Cambios |
| x = - 2 | + | - | - | + | 2 |
| Signos | f (x) | f1(x) | f2(x) | f3(x) | Cambios |
| x = - 1 | - | - | + | + | 1 |
| Signos | f (x) | f1(x) | f2(x) | f3(x) | Cambios |
| x = - 3 | + | + | - | + | 2 |
Por último, si se quiere verificar estos resultados (tal vez los resultados no están muy claros), veamos una tabla completa
| Signos | -  |
-4 | -3 | -2 | -1 | 0 | 1 | 2 | +  |
| f (x) | - | - | + | + | - | - | - | + | + |
| f1(x) | + | + | + | - | - | 0 | + | + | + |
| f2(x) | - | - | - | - | + | + | + | + | + |
| f3(x) | + | + | + | + | + | + | + | + | + |
| Cambios | 3 | 3 | 2 | 2 | 1 | 1 | 1 | 0 | 0 |
Revista Matemáticas, Educación
e Internetâ
Derechos Reservados