
1
2
3
4
5
6 7 8
Apéndice
Métodos para aproximar los ceros de un polinomio
Aunque existen muchos métodos para aproximar los ceros de un polinomio, aquí solo vamos a mencionar tres muy simples y conocidos: el método de la bisección, el método de bisección acelerada y el método de Newton. Si se quiere investigar más sobre estos métodos o buscar más se puede investigar en algún libro de Métodos Numéricos.
Método de bisección
Para poder utilizar este método se necesitan tener dos valores iniciales a y b tales que f (a) y f (b) tienen signo contrario. Una vez que se cumple esto, entonces tome
c=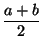 y evalúe f (c), si f (c) = 0 entonces ya se encontró que el cero es x = c, sino si f (a) y f (c) tienen signo contrario, entonces tome a = a y b = c y repita el proceso, sino tome a = c y b = b. El proceso se repite hasta que f (c) sea menor que un valor pequeño predeterminado, puede ser
f (c) < 0.00001.
y evalúe f (c), si f (c) = 0 entonces ya se encontró que el cero es x = c, sino si f (a) y f (c) tienen signo contrario, entonces tome a = a y b = c y repita el proceso, sino tome a = c y b = b. El proceso se repite hasta que f (c) sea menor que un valor pequeño predeterminado, puede ser
f (c) < 0.00001.
Método de bisección acelerada
Este método es similar al anterior, se necesitan dos valores iniciales a y b tales que f (a) y f (b) tengan diferente signo. La diferencia está en que ahora se toma
c=a-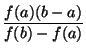 . Si f (c) = 0 entonces ya se encontró que el cero es x = c, sino si f (a) y f (c) tienen signo contrario, entonces tome a = a y b = c y repita el proceso, sino tome a = c y b = b. El proceso se termina cuando f (c) es menor que un valor pequeño predeterminado, talvez
f (c) = 0.00001.
. Si f (c) = 0 entonces ya se encontró que el cero es x = c, sino si f (a) y f (c) tienen signo contrario, entonces tome a = a y b = c y repita el proceso, sino tome a = c y b = b. El proceso se termina cuando f (c) es menor que un valor pequeño predeterminado, talvez
f (c) = 0.00001.
Método de Newton
Para este método solo se necesita un valor inicial a, el siguiente valor que se toma es
c=a-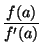 . Si f (c) = 0 entonces ya encontramos el cero, es x = c, sino se continúa el proceso hasta que f (c) sea menor que un valor pequeño predeterminado, puede ser
f (c) < 0.00001
. Si f (c) = 0 entonces ya encontramos el cero, es x = c, sino se continúa el proceso hasta que f (c) sea menor que un valor pequeño predeterminado, puede ser
f (c) < 0.00001
El problema que presentan estos métodos es que los valores iniciales deben ser muy buenos, el primer método es muy lento, el segundo es un poco más rápido y el tercero es el más sencillo y puede ser el más rápido, sin embargo, puede pasar que se pierda y nunca encuentre el cero. Si se realizan en un programa de computadora es conveniente que se ponga un número máximo de iteraciones por si nunca se llega a un resultado satisfactorio.
Corolario del Teorema de Rolle y la Regla de Descartes
TEOREMA 4
Corolario del Teorema de Rolle
Entre dos raíces reales consecutivas a y b de f (x) = 0, hay un número impar de raíces reales de f'(x) = 0, una raíz de multiplicidad m es contada m veces.
TEOREMA 5
La Regla de Descartes
El número de raíces reales positivas de una ecuacón real es igual al número v de sus variaciones de signo o es menor que v por un número entero positivo par. Una raíz de multiplicidad m se cuentan m veces.
Dickson, L. New First Course in the Theory of Equations.
Jhon Wiley and Sons, New York, 1962.
1
2
3
4
5
6 7 8
Revista Matemáticas, Educación
e Internetâ
Derechos Reservados
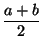 y evalúe f (c), si f (c) = 0 entonces ya se encontró que el cero es x = c, sino si f (a) y f (c) tienen signo contrario, entonces tome a = a y b = c y repita el proceso, sino tome a = c y b = b. El proceso se repite hasta que f (c) sea menor que un valor pequeño predeterminado, puede ser
f (c) < 0.00001.
y evalúe f (c), si f (c) = 0 entonces ya se encontró que el cero es x = c, sino si f (a) y f (c) tienen signo contrario, entonces tome a = a y b = c y repita el proceso, sino tome a = c y b = b. El proceso se repite hasta que f (c) sea menor que un valor pequeño predeterminado, puede ser
f (c) < 0.00001.

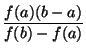 . Si f (c) = 0 entonces ya se encontró que el cero es x = c, sino si f (a) y f (c) tienen signo contrario, entonces tome a = a y b = c y repita el proceso, sino tome a = c y b = b. El proceso se termina cuando f (c) es menor que un valor pequeño predeterminado, talvez
f (c) = 0.00001.
. Si f (c) = 0 entonces ya se encontró que el cero es x = c, sino si f (a) y f (c) tienen signo contrario, entonces tome a = a y b = c y repita el proceso, sino tome a = c y b = b. El proceso se termina cuando f (c) es menor que un valor pequeño predeterminado, talvez
f (c) = 0.00001.
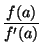 . Si f (c) = 0 entonces ya encontramos el cero, es x = c, sino se continúa el proceso hasta que f (c) sea menor que un valor pequeño predeterminado, puede ser
f (c) < 0.00001
. Si f (c) = 0 entonces ya encontramos el cero, es x = c, sino se continúa el proceso hasta que f (c) sea menor que un valor pequeño predeterminado, puede ser
f (c) < 0.00001