Introducción
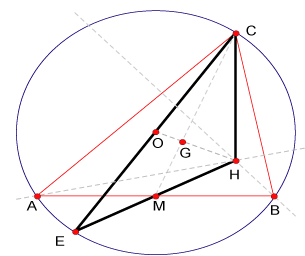
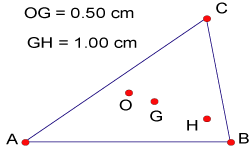
En los Elementos (Libro IV, Proposición 5) de Euclides ya figura la concurrencia de las mediatrices de los lados de un triángulo en el circuncentro. Es en obras de Arquímedes donde aparece la concurrencia de medianas (El equilibrio de los planos, Proposición 13) y alturas de un triángulo (Libro de los Lemas, Proposición 5) en baricentro y ortocentro respectivamente. Durante 2000 años estos puntos tuvieron una existencia independiente uno del otro. Habría que esperar a Leonard Euler (1707 + 76 = 1783) para reparar en que dichos puntos estaban alineados y por si fuera poco que la distancia del baricentro al ortocentro era el doble de la distancia del circuncentro al baricentro. El presente artículo busca responder a la siguiente interrogante: Cuál será la situación de estos puntos en un cuadrilátero?. Para ello tendremos que generalizar la idea de baricentro, circuncentro y ortocentro y buscar definirlos en un cuadrilátero. Empecemos por señalar que sólo tendrá sentido hablar de circuncentro de un cuadrilátero en el caso en que este sea inscriptible. Proposición 1 Demostración Aquí E el simétrico de C respecto de O, Entendiendo como baricentro de un segmento a su punto medio, definimos las
medianas de un triángulo como los segmentos que unen cada vértice del triángulo
con el baricentro del lado opuesto, se cumple la siguiente proposición. Proposición 2 Las medianas de un triángulo concurren en un punto que divide a cada mediana
en dos segmentos uno doble del otro. Demostración Las medianas
En resumen:
Procediendo de forma análoga: considerando que las medianas En resumen:
Por lo visto en Definición [Baricentro]. Llamaremos baricentro de un triángulo al punto de intersección de sus
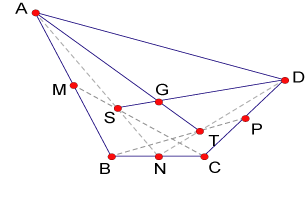
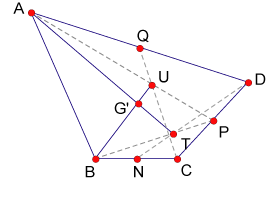
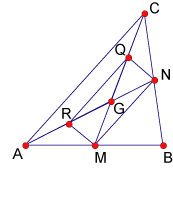
medianas. Definición [Medianas de un cuadrilátero]. Definimos las medianas de un cuadrilátero como los segmentos que unen cada
vértice con los baricentros de los triángulos que forman los tres vértices
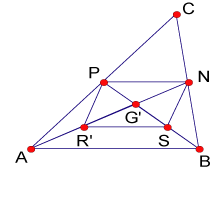
restantes. Proposición 3 Se cumple la siguiente proposición: Las medianas de un cuadrilátero concurren en un punto que divide a cada
mediana en dos segmentos uno triple del otro. Demostración Por lo demostrado acerca de las medianas de un triángulo se cumple que
Razonado de manera análoga, si las medianas
A partir de lo visto en
Definición [Baricentro de un cuadrilátero]. Llamaremos baricentro de un cuadrilátero al punto de intersección de sus medianas.
Cidse
- Revista
virtual Matemática, Educación e Internet -
ITCR
|
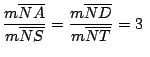 de donde por el recíproco de Tales podemos afirmar que
de donde por el recíproco de Tales podemos afirmar que 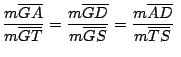 y como además
y como además
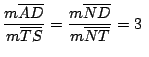 podemos concluir
que
podemos concluir
que