|
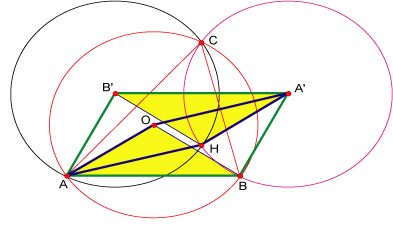
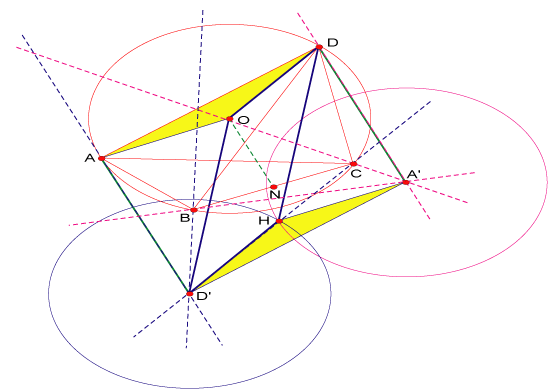
Proposición 4
Sea 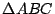 triángulo de circuncentro triángulo de circuncentro 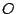 . Sean . Sean
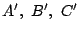 simétricos de simétricos de 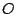 respecto de respecto de
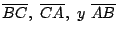 respectivamente, entonces las circunferencias respectivamente, entonces las circunferencias
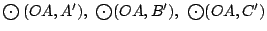 pasan por un mismo punto H. pasan por un mismo punto H.
Demostración
El cuadrilátero 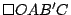 es rombo al igual que el cuadrilátero es rombo al igual que el cuadrilátero 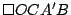 por lo que el cuadrilátero por lo que el cuadrilátero
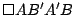 es paralelogramo, de donde es paralelogramo, de donde
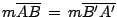 . .
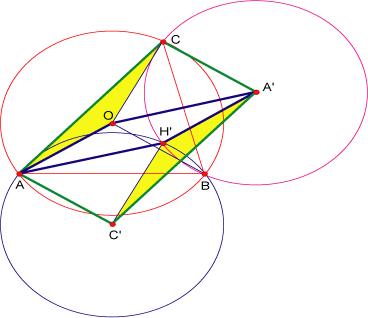
Las circunferencias
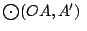 y y
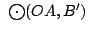 se cortan en se cortan en 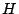 . .
Los triángulos 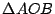 y y 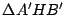 son congruentes por tener los tres lados congruentes y como además por ser son congruentes por tener los tres lados congruentes y como además por ser
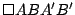 paralelogramo paralelogramo 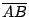 es paralela a es paralela a
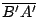 por lo que por lo que 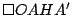 es paralelogramo. (1) es paralelogramo. (1)
Procediendo de forma análoga, el cuadrilátero 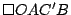 es rombo al igual que el cuadrilátero es rombo al igual que el cuadrilátero 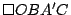 por lo que por lo que
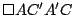 es paralelogramo, de donde es paralelogramo, de donde
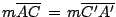 . .
Las circunferencias
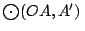 y y
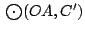 se cortan en se cortan en 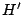 . .
Los triángulos 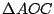 y y 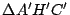 son congruentes por tener los tres lados congruentes y como además por ser son congruentes por tener los tres lados congruentes y como además por ser
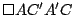 paralelogramo es paralelogramo es 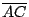 paralela a paralela a
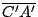 por lo que por lo que
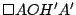 es paralelogramo. (2) es paralelogramo. (2)
En 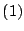 y y 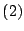 vimos que vimos que 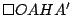 y y
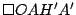 son paralelogramos que coinciden en tres de sus vértices por lo que debe ser son paralelogramos que coinciden en tres de sus vértices por lo que debe ser 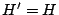 . .
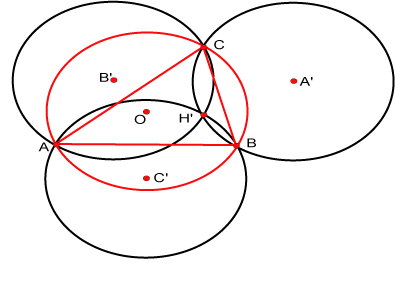
Definición [Ortocentro de un triángulo.]
Definimos como ortocentro del triángulo 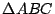 al punto H determinado en la propiedad anterior. al punto H determinado en la propiedad anterior.
Coincide el ortocentro del triángulo 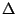 ABC definido de esta manera con el punto de intersección de sus alturas? ABC definido de esta manera con el punto de intersección de sus alturas?
Como
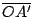 es perpendicular a es perpendicular a 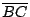 , al ser , al ser 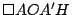 paralelogramo, se cumple que paralelogramo, se cumple que 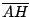 también es perpendicular a también es perpendicular a 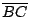 . De la misma forma . De la misma forma 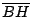 y y 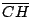 son perpendiculares a son perpendiculares a 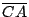 y y 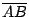 respectivamente. respectivamente. 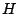 es entonces punto de intersección de las alturas de es entonces punto de intersección de las alturas de 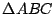 . .
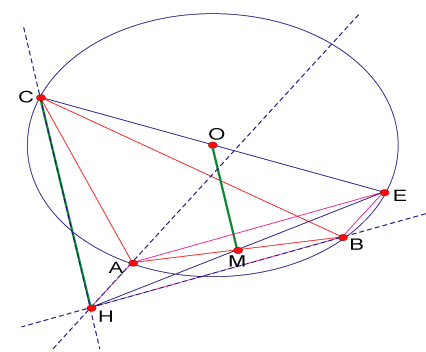
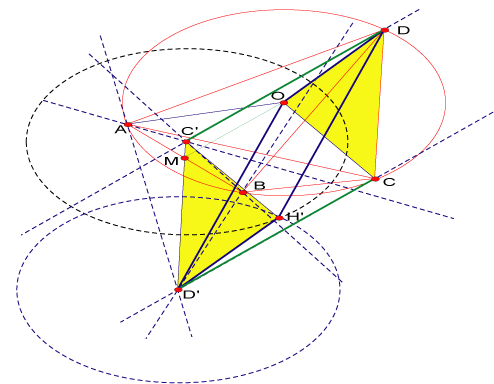
Proposición 5
Sea 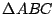 un triángulo cualquiera de ortocentro un triángulo cualquiera de ortocentro 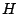 y circuncentro y circuncentro 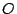 . Siendo . Siendo 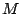 el punto medio de el punto medio de 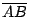 se cumple que se cumple que 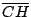 es paralelo a es paralelo a 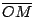 y y
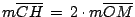 . .
Demostración
Si 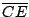 es diámetro de es diámetro de 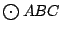 se cumple: se cumple: 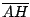 y y 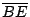 son paralelas por ser ambas perpendiculares a son paralelas por ser ambas perpendiculares a 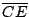 , al igual que , al igual que 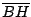 y y 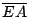 son paralelas por ser ambas perpendiculares a son paralelas por ser ambas perpendiculares a 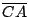 , entonces , entonces 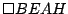 es paralelogramo y como es paralelogramo y como 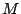 es punto medio de es punto medio de 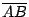 también también 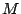 es punto medio de es punto medio de 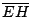 y como y como 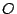 es punto medio de es punto medio de 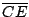 se cumple que se cumple que 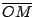 es paralelo a es paralelo a 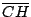 y y
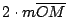 . .
Proposición 6
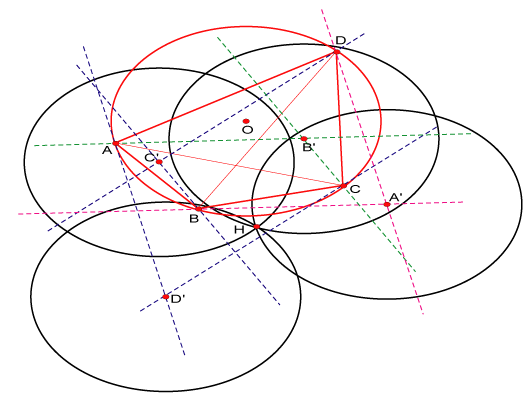
Sea 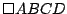 un cuadrilátero inscrito en un cuadrilátero inscrito en
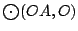 , ,
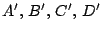 ortocentros de ortocentros de 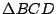 , , 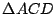 , , 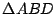 , , 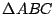 respectivamente. Las circunferencias respectivamente. Las circunferencias
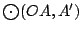 , ,
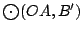 , ,
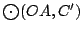 , ,
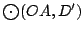 pasan por un mismo punto pasan por un mismo punto 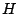 . .
Demostración
Sean 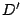 y y 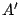 ortocentros de ortocentros de 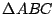 y y 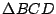 respectivamente. Si respectivamente. Si 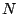 es el punto medio de es el punto medio de 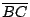 , por lo demostrado previamente , por lo demostrado previamente
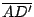 es paralela a es paralela a 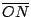 y y
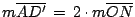 , y también , y también
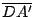 es paralela a es paralela a 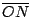 y y
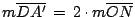 por lo que por lo que
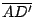 es paralela a es paralela a
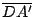 y y
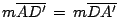 de donde de donde
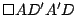 es paralelogramo y por lo tanto es paralelogramo y por lo tanto
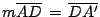 . .
Las circunferencias
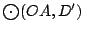 y y
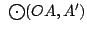 se cortan en se cortan en  y otro punto. y otro punto.
Los triángulos
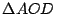 y y
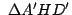 son iguales por tener los tres lados iguales, entonces son iguales por tener los tres lados iguales, entonces 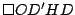 es paralelogramo. es paralelogramo. 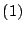
Procediendo de forma análoga, 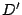 y y 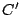 ortocentros de ortocentros de 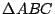 y y 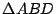 respectivamente. respectivamente.
Si 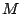 es el punto medio de es el punto medio de 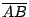 , por lo demostrado previamente , por lo demostrado previamente
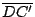 es paralela a es paralela a 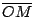 y y
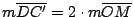 , y también , y también
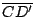 es paralela a es paralela a 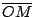 y y
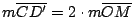 por lo que por lo que
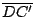 es paralela a es paralela a
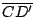 y y
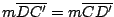 de donde de donde
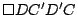 es paralelogramo y por lo tanto es paralelogramo y por lo tanto
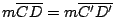 . .
Las circunferencias
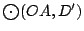 y y
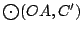 se cortan en se cortan en 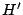 . .
Los triángulos 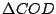 y y 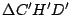 son iguales, entonces son iguales, entonces
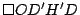 es paralelogramo. es paralelogramo. 
En resumen: por lo demostrado en 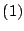 y y 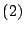 los cuadriláteros los cuadriláteros 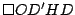 y y
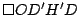 son paralelogramos que coinciden en tres de sus vértices, por lo tanto debe ser son paralelogramos que coinciden en tres de sus vértices, por lo tanto debe ser 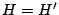 . .
Razonando de la misma manera podemos demostrar que
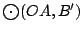 siendo siendo 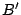 ortocentro de ortocentro de 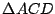 , pasa por , pasa por 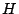 . .
Definición [Ortocentro de un cuadrilátero.]
Definimos como ortocentro del cuadrilátero inscriptible 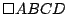 al punto al punto 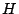 determinado en la propiedad anterior. determinado en la propiedad anterior.
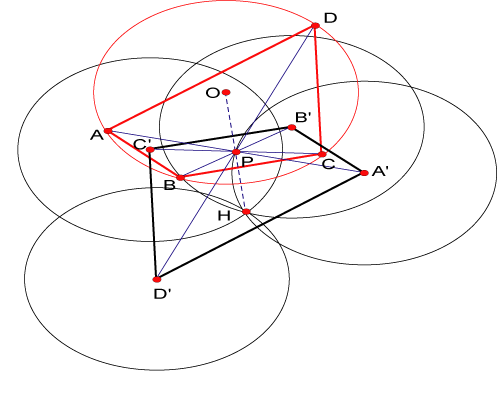
Los cuadriláteros 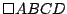 y y
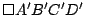 , al igual que , al igual que 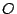 y y 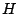 sus circuncentros respectivos se corresponden en una simetría central de centro sus circuncentros respectivos se corresponden en una simetría central de centro 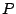 , punto de intersección de , punto de intersección de
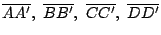 . .
De los visto hasta el momento
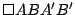 , ,
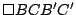 , ,
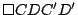 , ,
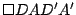 son paralelogramos por lo que los segmentos son paralelogramos por lo que los segmentos
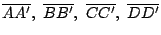 tienen punto medio común tienen punto medio común 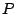 . .
Los cuadriláteros 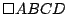 y y
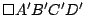 se corresponden entonces en una simetría central de centro se corresponden entonces en una simetría central de centro 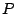 . .
También se corresponden en la misma simetría central los puntos 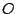 y y 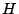 , circuncentros de , circuncentros de 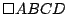 y y
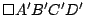 respectivamente, por lo que respectivamente, por lo que 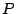 es punto medio de es punto medio de 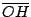 . .
Cidse - Revista virtual Matemática, Educación e Internet - ITCR
Derechos Reservados
|