|
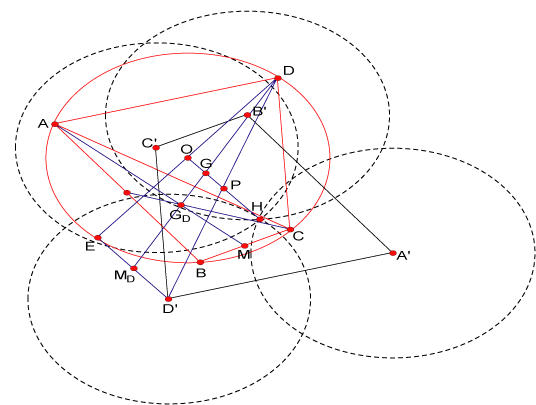
Recta de Euler en cuadriláteros
Proposición 7 El circuncentro Demostración Entonces de
Entonces de
Entonces de
Si
Entonces de
Si
Entonces de
Entonces de
Cidse - Revista virtual Matemática, Educación e Internet - ITCR
|