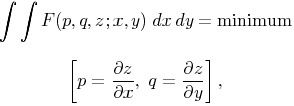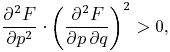1 2 3 4 5 6 7 8 9 10 |
19.
Are the solutions of regular problems in the calculus of variations
always necessarily analytic?
One
of the most remarkable facts in the elements of the theory of analytic
functions appears to me to be this: That there exist partial differential
equations whose integrals are all of necessity analytic functions of the
independent variables, that is, in short, equations susceptible of none
but analytic solutions. The best known partial differential equations of
this kind are the potential equation
and certain linear
differential equations investigated by Picard;46
also the equation
the partial
differential equation of minimal surfaces, and others. Most of these
partial differential equations have the common characteristic of being
the lagrangian differential equations of certain problems of variation,
viz., of such problems of variation
as satisfy, for all
values of the arguments which fall within the range of discussion, the
inequality
F
itself being an analytic function. We shall call this sort of problem a
regular variation problem. It is chiefly the regular variation problems
that play a role in geometry, in mechanics, and in mathematical physics;
and the question naturally arises, whether all solutions of regular
variation problems must necessarily be analytic functions. In other words,
does every lagrangian partial differential equation of a regular
variation problem have the property of admitting analytic integrals
exclusively? And is this the case even when the function is
constrained to assume, as, e. g., in Dirichlet's problem on the
potential function, boundary values which are continuous, but not
analytic? I
may add that there exist surfaces of constant negative gaussian
curvature which are representable by functions that are continuous and
possess indeed all the derivatives, and yet are not analytic; while on
the other hand it is probable that every surface whose gaussian curvature
is constant and positive is necessarily an analytic surface. And we know
that the surfaces of positive constant curvature are most closely related
to this regular variation problem: To pass through a closed curve in
space a surface of minimal area which shall inclose, in connection with a
fixed surface through the same closed curve, a volume of given magnitude.
20.
The general problem of boundary values
An
important problem closely connected with the foregoing is the question
concerning the existence of solutions of partial differential equations
when the values on the boundary of the region are prescribed. This
problem is solved in the main by the keen methods of H. A. Schwarz, C.
Neumann, and Poincaré for the differential equation of the potential.
These methods, however, seem to be generally not capable of direct
extension to the case where along the boundary there are prescribed
either the differential coefficients or any relations between these and
the values of the function. Nor can they be extended immediately to the
case where the inquiry is not for potential surfaces but, say, for
surfaces of least area, or surfaces of constant positive gaussian
curvature, which are to pass through a prescribed twisted curve or to
stretch over a given ring surface. It is my conviction that it will be
possible to prove these existence theorems by means of a general
principle whose nature is indicated by Dirichlet's principle. This
general principle will then perhaps enable us to approach the question: Has
not every regular variation problem a solution, provided certain
assumptions regarding the given boundary conditions are satisfied (say
that the functions concerned in these boundary conditions are continuous
and have in sections one or more derivatives), and provided also if
need be that the notion of a solution shall be suitably extended?47 21.
Proof of the existence of linear differential equations having a
prescribed monodromic group
In
the theory of linear differential equations with one independent variable
z, I wish to indicate an important problem one which very likely
Riemann himself may have had in mind. This problem is as follows: To
show that there always exists a linear differential equation of the
Fuchsian class, with given singular points and monodromic group. The
problem requires the production of n functions of the variable z,
regular throughout the complex z-plane except at the given
singular points; at these points the functions may become infinite of
only finite order, and when z describes circuits about these
points the functions shall undergo the prescribed linear substitutions.
The existence of such differential equations has been shown to be
probable by counting the constants, but the rigorous proof has been
obtained up to this time only in the particular case where the
fundamental equations of the given substitutions have roots all of
absolute magnitude unity. L. Schlesinger has given this proof,48 based upon Poincaré's theory of the Fuchsian
22.
Uniformization of analytic relations by means of automorphic functions
As
Poincaré was the first to prove, it is always possible to reduce any
algebraic relation between two variables to uniformity by the use of
automorphic functions of one variable. That is, if any algebraic equation
in two variables be given, there can always be found for these variables
two such single valued automorphic functions of a single variable that
their substitution renders the given algebraic equation an identity. The
generalization of this fundamental theorem to any analytic non-algebraic
relations whatever between two variables has likewise been attempted with
success by Poincaré,49 though by a way entirely different from that which served him in the
special problem first mentioned. From Poincaré's proof of the
possibility of reducing to uniformity an arbitrary analytic relation
between two variables, however, it does not become apparent whether the
resolving functions can be determined to meet certain additional
conditions. Namely, it is not shown whether the two single valued
functions of the one new variable can be so chosen that, while this
variable traverses the regular domain of those functions, the totality of
all regular points of the given analytic field are actually reached and
represented. On the contrary it seems to be the case, from Poincaré's
investigations, that there are beside the branch points certain others,
in general infinitely many other discrete exceptional points of the
analytic field, that can be reached only by making the new variable
approach certain limiting points of the functions. In view of the
fundamental importance of Poincaré's formulation of the question it
seems to me that an elucidation and resolution of this difficulty is
extremely desirable. In
conjunction with this problem comes up the problem of reducing to
uniformity an algebraic or any other analytic relation among three or
more complex variables--a problem which is known to be solvable in many
particular cases. Toward the solution of this the recent investigations
of Picard on algebraic functions of two variables are to be regarded as
welcome and important preliminary studies. |