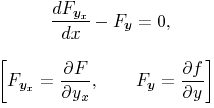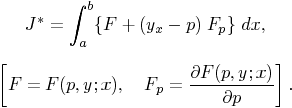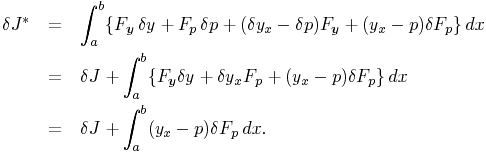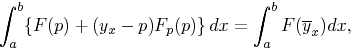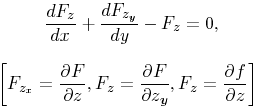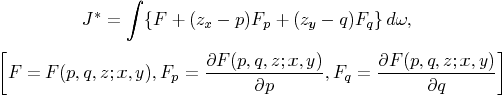1 2 3 4  5 6 7 8 9 10

23. Further development of the methods of the calculus of variations

So far, I have generally mentioned problems as definite and special as possible, in the opinion that it is just such definite and special problems that attract us the most and from which the most lasting influence is often exerted upon science. Nevertheless, I should like to close with a general problem, namely with the indication of a branch of mathematics repeatedly mentioned in this lecture--which, in spite of the considerable advancement lately given it by Weierstrass, does not receive the general appreciation which, in my opinion, is its due--I mean the calculus of variations.⁵⁰

The lack of interest in this is perhaps due in part to the need of reliable modern text books. So much the more praiseworthy is it that A. Kneser in a very recently published work has treated the calculus of variations from the modern points of view and with regard to the modern demand for rigor.⁵¹

The calculus of variations is, in the widest sense, the theory of the variation of functions, and as such appears as a necessary extension of the differential and integral calculus. In this sense, Poincaré's investigations on the problem of three bodies, for example, form a chapter in the calculus of variations, in so far as Poincaré derives from known orbits by the principle of variation new orbits of similar character.

I add here a short justification of the general remarks upon the calculus of variations made at the beginning of my lecture.

The simplest problem in the calculus of variations proper is known to consist in finding a function y of a variable x such that the definite integral

assumes a minimum value as compared with the values it takes when y is replaced by other functions of x with the same initial and final values.

The vanishing of the first variation in the usual sense

J = 0

gives for the desired function y the well-known differential equation

In order to investigate more closely the necessary and sufficient criteria for the occurrence of the required minimum, we consider the integral

Now we inquire how p is to be chosen as function of x, y in order that the value of this integral J* shall be independent of the path of integration, i. e., of the choice of the function y of the variable x. The integral J* has the form

where A and B do not contain y, and the vanishing of the first variation

J* = 0

in the sense which the new question requires gives the equation

i. e., we obtain for the function p of the two variables x, y the partial differential equation of the first order

The ordinary differential equation of the second order (l) and the partial differential equation (1*) stand in the closest relation to each other. This relation becomes immediately clear to us by the following simple transformation

We derive from this, namely, the following facts: If we construct any simple family of integral curves of the ordinary differential equation (l) of the second order and then form an ordinary differential equation of the first order

which also admits these integral curves as solutions, then the function p(x, y) is always an integral of the partial differential equation (1*) of the first order; and conversely, if p(x, y) denotes any solution of the partial differential equation (1*) of the first order, all the non-singular integrals of the ordinary differential equation (2) of the first order are at the same time integrals of the differential equation (l) of the second order, or in short if y_x = p(x, y) is an integral equation of the first order of the differential equation (l) of the second order, p(x, y) represents an integral of the partial differential equation (1*) and conversely; the integral curves of the ordinary differential equation of the second order are therefore, at the same time, the characteristics of the partial differential equation (1*) of the first order.

In the present case we may find the same result by means of a simple calculation; for this gives us the differential equations (1) and (1*) in question in the form

where the lower indices indicate the partial derivatives with respect to x, y, p, y_x. The correctness of the affirmed relation is clear from this.

The close relation derived before and just proved between the ordinary differential equation (1) of the second order and the partial differential equation (1*) of the first order, is, as it seems to me, of fundamental significance for the calculus of variations. For, from the fact that the integral J* is independent of the path of integration it follows that

if we think of the left hand integral as taken along any path y and the right hand integral along an integral curve of the differential equation

With the help of equation (3) we arrive at Weierstrass's formula

where E designates Weierstrass's expression, depending upon y_x, p, y, x,

E(y_x, p) = F(y_x) - F(p) - (y_x - p) F_p(p),

Since, therefore, the solution depends only on finding an integral p(x, y) which is single valued and continuous in a certain neighborhood of the integral curve , which we are considering, the developments just indicated lead immediately--without the introduction of the second variation, but only by the application of the polar process to the differential equation (1)--to the expression of Jacobi's condition and to the answer to the question: How far this condition of Jacobi's in conjunction with Weierstrass's condition E > 0 is necessary and sufficient for the occurrence of a minimum.

The developments indicated may be transferred without necessitating further calculation to the case of two or more required functions, and also to the case of a double or a multiple integral. So, for example, in the case of a double integral

to be extended over a given region , the vanishing of the first variation (to be understood in the usual sense)

J = 0

gives the well-known differential equation of the second order

for the required function z of x and y.

On the other hand we consider the integral

and inquire, how p and q are to be taken as functions of x, y and z in order that the value of this integral may be independent of the choice of the surface passing through the given closed twisted curve, i. e., of the choice of the function z of the variables x and y.

The integral J* has the form

>and the vanishing of the first variation

J = 0

in the sense which the new formulation of the question demands, gives the equation

i. e., we find for the functions p and q of the three variables x, y and z the differential equation of the first order

If we add to this differential equation the partial differential equation

resulting from the equations

z_x = p(x, y, z),
z_y = q(x, y, z)

the partial differential equation (I) for the function z of the two variables x and y and the simultaneous system of the two partial differential equations of the first order (I*) for the two functions p and q of the three variables x, y, and z stand toward one another in a relation exactly analogous to that in which the differential equations (1) and (1*) stood in the case of the simple integral.

It follows from the fact that the integral J* is independent of the choice of the surface of integration z that

if we think of the right hand integral as taken over an integral surface z of the partial differential equations

and with the help of this formula we arrive at once at the formula

[E(z_x, z_y, p, q) = F(z_x, z_y) - F(p, q) - (z_x - p)F_p(p, q) -
(z_y - q)F_q(p)F_p(p, q)],

which plays the same role for the variation of double integrals as the previously given formula (4) for simple integrals. With the help of this formula we can now answer the question how far Jacobi's condition in conjunction with Weierstrass's condition E > 0 is necessary and sufficient for the occurrence of a minimum.

Connected with these developments is the modified form in which A. Kneser,⁵² beginning from other points of view, has presented Weierstrass's theory. While Weierstrass employed integral curves of equation (1) which pass through a fixed point in order to derive sufficient conditions for the extreme values, Kneser on the other hand makes use of any simple family of such curves and constructs for every such family a solution, characteristic for that family, of that partial differential equation which is to be considered as a generalization of the Jacobi-Hamilton equation.

The problems mentioned are merely samples of problems, yet they will suffice to show how rich, how manifold and how extensive the mathematical science of today is, and the question is urged upon us whether mathematics is doomed to the fate of those other sciences that have split up into separate branches, whose representatives scarcely understand one another and whose connection becomes ever more loose. I do not believe this nor wish it. Mathematical science is in my opinion an indivisible whole, an organism whose vitality is conditioned upon the connection of its parts. For with all the variety of mathematical knowledge, we are still clearly conscious of the similarity of the logical devices, the relationship of the ideas in mathematics as a whole and the numerous analogies in its different departments. We also notice that, the farther a mathematical theory is developed, the more harmoniously and uniformly does its construction proceed, and unsuspected relations are disclosed between hitherto separate branches of the science. So it happens that, with the extension of mathematics, its organic character is not lost but only manifests itself the more clearly.

But, we ask, with the extension of mathematical knowledge will it not finally become impossible for the single investigator to embrace all departments of this knowledge? In answer let me point out how thoroughly it is ingrained in mathematical science that every real advance goes hand in hand with the invention of sharper tools and simpler methods which at the same time assist in understanding earlier theories and cast aside older more complicated developments. It is therefore possible for the individual investigator, when he makes these sharper tools and simpler methods his own, to find his way more easily in the various branches of mathematics than is possible in any other science.

The organic unity of mathematics is inherent in the nature of this science, for mathematics is the foundation of all exact knowledge of natural phenomena. That it may completely fulfil this high mission, may the new century bring it gifted masters and many zealous and enthusiastic disciples!