1. Todos los habitantes de una pequeña isla están agrupados en sectas, y en dicha isla se cumplen las siguientes características:

1. En la isla existen al menos dos sectas.

2. En cada secta hay exactamente tres habitantes.

3. Cada dos sectas distintas tienen exactamente un habitante en común.

4. Por cada par de habitantes distintos, existe exactamente una secta a la que ambos pertenecen.

Encuentre la cantidad de habitantes en la isla.

 

Solución

Por (a) debe haber al menos cuatro habitantes, digamos 1, 2, 3 y 4. Supongamos que una de las sectas es S₁:1-2-3. Por (d) deben existir sectas S₂, S₃ y S₄, en las que están los habitantes 1-4, 2-4 y 3-4 respectivamente. S₁, S₂ y S₃ deben ser distintas, de hecho, si 2-4 y 3-4 están en la misma secta S₃, entonces S₃ : 2 - 3 - 4. Luego, S₁ y S₃ tendrían en común 2 habitantes, y eso es imposible. Nuevamente por (c), cada una de las sectas S₂, S₃ y S₄ tienen exactamente un habitante en común con S₁:1-2-3. Como no pueden haber 2 personas entre 1, 2 y 3 que están en S₂, S₃ y S₄, nuevamente por (c) debemos tener que S₂=1-4-a, S₃=2-4-b y S₄=3-4-c, para personas distintas a, b y c, que son a su vez distintas de 1, 2, 3 y 4. Con esto probamos que hay por lo menos 7 habitantes. Para mantener la consistencia, a, b y c son 5, 6 y 7; y S₂=1-4-5, S₃=2-4-6 y S₄=3-4-7.

Ahora supongamos que existe por lo menos un habitante más, digamos 8. Por (c) existe una secta S a la que pertenecen 1 y 8. Como S debe tener un miembro común con S₃=2-4-6 concluimos que S debe ser igual a 1-2-8, 1-4-8 o 1-6-8; y ninguna de estas es posible.

 

2. En un pueblo hay tres tipos de personas: los A, que siempre dicen la verdad; los B, que siempre mienten; y los C, que dicen alternadamente una verdad y una mentira, aunque nunca se sabe por cual de las dos comienzan.

Dos personas del pueblo, cada una de las cuales afirmaba que la otra era del tipo C, informaron a la prensa, después de observar una carrera con tres participantes los siguiente:

Persona #1: Ganó el número 120, el número 147 quedó de segundo, y el número 315 quedó tercero.

Persona #2: Ganó el número 315, segundo fue el número 120 y tercero el número 147.

Quién ganó la carrera?

 

Solución

Notemos primero que ninguna de las personas es tipo A, ya que si alguna de las personas es tipo A, la otra es tipo C (la primera afirmación), y entonces deberían coincidir en alguna de las posiciones de los competidores y esto no sucede.

Si algunas de las personas es tipo C, la otra estaría diciendo la verdad al afirmar que la otra persona era tipo C y como no puede ser tipo A, debe ser tipo C.

Ambos iniciaron con una verdad, así que su tercera afirmación debería ser verdad y debería conicidir, pero no es así. Entonces, ninguna de las dos personas es tipo C.

Así, ambos son tipo B y ninguna de sus afirmaciones es verdad, de ahí que el ganador de la carrera fue el número 147.

 

3. Sean m y n enteros positivos tales que 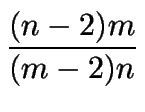= 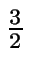. Determinar todos los pares ordenados (m, n) que verifican esta relación.

 

Solución

De la expresión da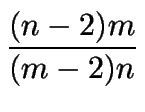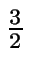da = , se da:

		2(n - 2)m = 2(m - 2)n
		2nm - 4m = 3mn - 6n
		-2nm + 3mn + 4m - 6n = 0
		mn - 6n + 4m = 0
		(m - 6)(n + 4) + 24 = 0

el problema consiste en hallar las soluciones enteras positivas de

(m - 6)(n + 4) = - 24

como -24 < 0 y (n + 4) > 0, debe ser que (m - 6) < 0 y divisores de 24.

Los posibles valores de m son: 5, 4 y 3.

Si m = 5, n + 4 = 24 n = 20.

Si m = 4, n + 4 = 12 n = 8.

Si m = 3, n + 4 = 8 n = 4.

Así que los posibles valores del par son: (5, 29), (4, 8) y (3, 4).

 

 1 2 3 4