10. Sea ABCD un cuadrilátero convexo como el de la figura, en el que:
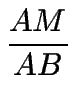 =
= 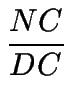
Probar que
(PMQN) = (APD) + (BQC).
Solución
Sea
r = 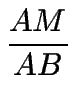 ,
entonces AM = r AB, y por condición del problema
,
entonces AM = r AB, y por condición del problema
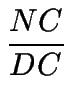 = r, se sigue NC = r DC.
= r, se sigue NC = r DC.
 ARR
ARR
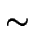
 AMR.
De la semejanza
AMR.
De la semejanza
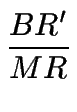 =
= 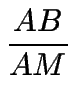 ,
es decir
,
es decir
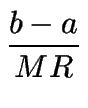 =
= 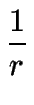 ,
de donde MR = r(b - a)
,
de donde MR = r(b - a)
|
m
|
=
|
a + RM
|
|
|
|
=
|
a + r(b - a)
|
|
|
|
=
|
(1 - r)a + rb(**)
|
|
|
(ADN) = 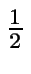 a DN a DN
|
|
|
(1)
|
|
(MDC) = 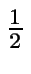 m DC m DC
|
|
|
(2)
|
|
(BNC) = 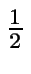 b NC
= b NC
= 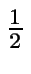 br DC br DC
|
|
|
(3)
|
pero
DN + NC = DC  DN = DC - NC = DC - r DC = (1
- r)DC.
DN = DC - NC = DC - r DC = (1
- r)DC.
Por lo tanto en (1)
|
(ADN) = 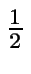 a(1
- r)DC a(1
- r)DC
|
|
|
(4)
|
Luego
|
(ADN) + (BNC)
|
=
|
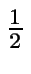 a(1
- r)DC + a(1
- r)DC + 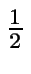 br DC br DC
|
|
|
|
=
|
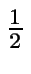 {a(1
- r) + br}DC {a(1
- r) + br}DC
|
|
|
|
=
|
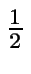 m DC m DC
|
|
|
|
=
|
(MDC)
|
|
Finalmente
|
(PMQN)
|
=
|
(DMC) - [(DPN) + (NQC)]
|
|
|
|
=
|
(ADN) + (BNC) - (DPN) -
(NQC)
|
|
|
|
=
|
(ADP) + (BQC)
|
|
11. Considere los números de la forma:
m = 
Pruebe que m es divisible por 81.
Solución
m es divisible por 3, pues la suma de los dígitos
27 . k . 3 es divisible por 3. Luego:
Además,
111111111÷9 = 12 345 679. Luego, reescribiendo la expresión
anterior se obtiene:
m = 3 . 9 . ( 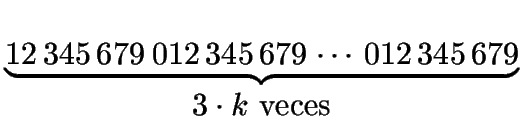 ).
).
Luego, como todos los dígitos se repiten 3k veces, se tiene que el número
que se encuentra dentro del paréntesis es divisible por 3. Luego, m
es divisible por 81.
12. Determine todos los pares (a, b) de enteros positivos, tales
que ab2 + b + 7 divide a a2b
+ a + b.
Solución
Sea
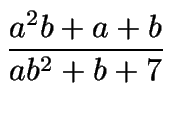 el entero dado.
el entero dado.
Luego,
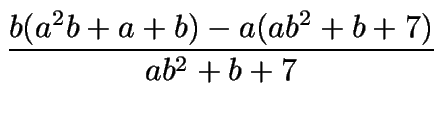 =
= 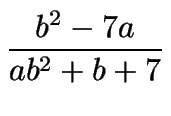 es un entero.
es un entero.
Como
b2 - 7a < b2 < ab2
+ b + 7 tenemos que
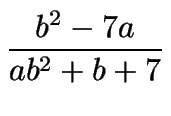 < 1.
< 1.
Si
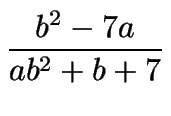 = 0, se tiene entonces que b2 = 7a, donde b
es múltiplo de 7 (digamos b = 7t), y (7t)2
= 7a nos da a = 7t2. Es fácil ver que
(a, b) = (7t2, 7t) satisface las
condiciones del enunciado par todo t entero positivo, tenemos en este
caso
= 0, se tiene entonces que b2 = 7a, donde b
es múltiplo de 7 (digamos b = 7t), y (7t)2
= 7a nos da a = 7t2. Es fácil ver que
(a, b) = (7t2, 7t) satisface las
condiciones del enunciado par todo t entero positivo, tenemos en este
caso
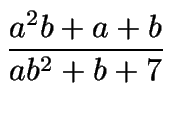 = t.
= t.
Si
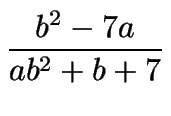 < 0, debemos tener b2 < 7a, y
< 0, debemos tener b2 < 7a, y
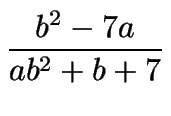
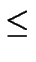 - 1 (pues es un entero), y por lo tanto
7a > 7a - b2
- 1 (pues es un entero), y por lo tanto
7a > 7a - b2 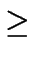 ab2 + b + 7
ab2 + b + 7  7a > ab2
7a > ab2  b2 < 7
b2 < 7  b = 1 o b = 2.
b = 1 o b = 2.
Sea b = 1,
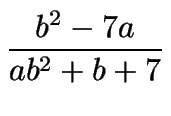 =
= 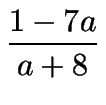 = - 7 +
= - 7 + 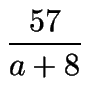 ,
y debemos ver que a + 8 divide a 57, como a es un entero
positivo
,
y debemos ver que a + 8 divide a 57, como a es un entero
positivo
 a + 8 = 19 o a + 8 = 19 o
a + 8 = 57
a + 8 = 19 o a + 8 = 19 o
a + 8 = 57  a = 11 o a = 49. Para a = 11 y b = 1 tenemos
que:
a = 11 o a = 49. Para a = 11 y b = 1 tenemos
que:
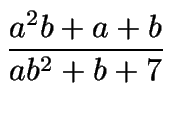 =
= 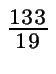 = 7
= 7
y para a = 49 y b = 1, tenemos:
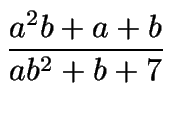 =
= 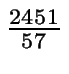 = 43
= 43
Si b = 2,
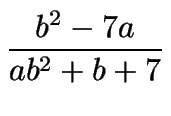 =
= 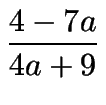 .
.
Como
4 - 7a > - 18 - 8a = - 2(4a + 9), si
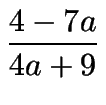 es un entero negativo, debemos tener
es un entero negativo, debemos tener
Así, las soluciones son dadas por
(a, b) = (7t2, 7a), t 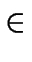 IN; (a, b) = (11, 1) y
(a, b) = (49, 1).
IN; (a, b) = (11, 1) y
(a, b) = (49, 1).

