4. Sea ABC un triángulo equilátero. Se
construye un cuadrado en el exterior del triángulo, usando el lado
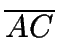 .
Si D es un punto del interior del
.
Si D es un punto del interior del
 ABC
tal que
m
ABC
tal que
m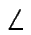 ADB
= 150, y
ADB
= 150, y
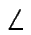 EBC
EBC
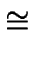
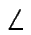 ABD.
Calcule el valor de la razón
ABD.
Calcule el valor de la razón
Solución
De acuerdo con la figura anterior, como
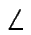 FCA
= 90o y
FCA
= 90o y
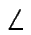 ACB
= 60o, entonces:
ACB
= 60o, entonces:
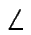 FCB
=
FCB
= 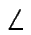 ADB
= 150o, y por ser
ADB
= 150o, y por ser
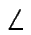 FBC)
FBC)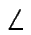 ABD,
se obtiene por ángulo-ángulo que
ABD,
se obtiene por ángulo-ángulo que
 FCB
FCB
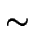
 ADB,
y por lo tanto
ADB,
y por lo tanto
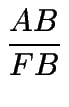 =
= 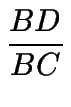 (1)
(1)
Ahora, como
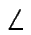 ABD
=
ABD
= 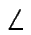 FBC
y
FBC
y
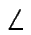 DBF
=
DBF
= 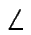 DBF
entonces se tiene que
DBF
entonces se tiene que
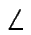 ABF
=
ABF
= 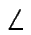 DBC (2)
DBC (2)
De (1) y (2) se deduce por criterio de semejanza lado-ángulo-lado
que
 ABF
ABF
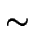
 DBC
y
DBC
y
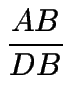 =
= 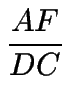 ,
entonces
,
entonces
AB . DC = DB . AF
(3)
Como AF es la diagonal del cuadrado ACFE, se
tiene que
AF = AC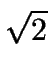 ,
y sustituyendo en (3) se obtiene
AB . DC = DB . AC
,
y sustituyendo en (3) se obtiene
AB . DC = DB . AC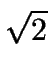 .
Finalmente, la razón pedida se puede escribir entonces como
.
Finalmente, la razón pedida se puede escribir entonces como
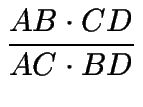 =
= 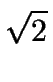 .
.
5. Sea
 ABC
un triángulo tal que el círculo S de diámetro
ABC
un triángulo tal que el círculo S de diámetro
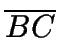 pasa por el punto medio M de AB, AC es tangente a S.
Sea N el punto diametralmente opuesto a M sobre S. Pruebe
que la razón de las áreas entre los triángulos
pasa por el punto medio M de AB, AC es tangente a S.
Sea N el punto diametralmente opuesto a M sobre S. Pruebe
que la razón de las áreas entre los triángulos
 ABC
y
ABC
y
 MNC
es 2.
MNC
es 2.
Solución
Considere la figura adjunta. Sea O el centro del círculo y x
la medida de AM, entonces
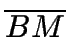 = x, porque M es punto medio.
= x, porque M es punto medio.
El triángulo
 ABC
es rectángulo en C, porque
AC
ABC
es rectángulo en C, porque
AC 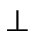 OC (radio)
OC (radio)
 AC
AC 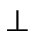 BC.
BC.
Sea r el radio de S. Como O y M son puntos
medios de BC y AB respectivamente,
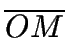 es la paralela media del triángulo
es la paralela media del triángulo
 ABC
y
AC = 2 OM = 2r, de donde
ABC
y
AC = 2 OM = 2r, de donde
 ABC
es un triángulo rectángulo isóceles.
ABC
es un triángulo rectángulo isóceles.
Además,
OC 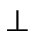 MN porque
MN || AC y
AC
MN porque
MN || AC y
AC 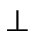 OC.
OC.
Así:
6. Determine el máximo valor para la expresión:
si x + y + z = 8 y
xy + xz + yz = 10.
Solución
Primero note que si x + y + z = 8 y
xy + xz + yz = 10, entonces:
| |
|
(x + y + z)2 =
x2 + y2 + z2 +
2(xy + xz + yz) |
|
| |
 |
(x + y + z)2 =
x2 + y2 + z2 +
20 |
|
| |
 |
x2 + y2 +
20 = (x + y + z)2 - z2 |
|
| |
 |
x2 + y2 +
20 = (x + y)(x + y + 2z) |
|
En forma análoga se tiene que
x2 + z2 + 20 = (x + z)(x
+ z + 2y) y
(y2 + z2 + 20 = (y + z)(y
+ z + 2x). Por lo que:
se convierte en:
(x + y + 2z) + (x + z + 2y) + (y
+ z + 2x) = 4(x + y + z) = 32.

