1 2 3 4

7. Para cuáles valores de x, y y z la expresión x² + 2xz + 2xy - 4x + z² + 2yz - 4z + y² - 4y - 5 tiene su valor mínimo, si se sabe que x + z = 2(4 + y) y x(z - y) = 3?

Solución

La expresión x² + 2xz + 2xy - 4x + z² + 2yz - 4z + y² - 4y - 5 se puede escribir como:
(x + y + z + 1)(x + y + z - 5)
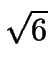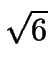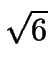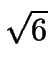Entonces si llamamos t = x + y + z, tenemos la expresión cuadrática en t : (t + 1)(t - 5), que alcanza su valor mínimo en t = 2. Así x + y + z = 2. Por otro lado, como x + z = 2(4 + y) y x(z - y) = 3, se obtiene que x = 3 - $\sqrt{6}$ , y = - 2 y z = 1 + $\sqrt{6}$ ; o bien x = 3 + $\sqrt{6}$ , y = - 2 y z = 1 - $\sqrt{6}$ .

8. La sucesión creciente 2, 3, 5, 6, 7, 10, 11,... consta de todos los números enteros positivos que no son ni el cuadrado ni el cubo de un entero positivo. Hallar el término que ocupa el puesto 500 en esta sucesión.

Solución
Entre 1 y 500 hay [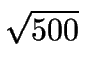 $\sqrt{500}$ ] = 22 cuadrados perfectos y [ $\sqrt[3]{500}$ ] = 7 cubos perfectos. Entre estos enteros hay [ $\sqrt[6]{500}$ ] = 2 de ellos (1 y 64) que se han contado dos veces. Luego, hay 22 + 7 - 2 = 27 enteros entre 1 y 500 que no están en la sucesión. Para encontrar el término 500 debemos añadir 27 enteros a la lista 2, 3, 5,..., 500 de 473 números no cuadrados y no cubos. Como no podemos usar 512, el último número será 528.

9. Sean a, b y c números reales positivos tales que abc = 1. Pruebe que:

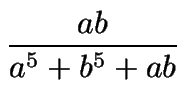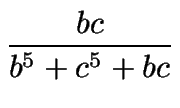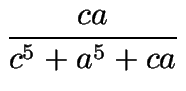
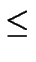$\displaystyle {\frac{ab}{a^5+b^5+ab}}$ + $\displaystyle {\frac{bc}{b^5+c^5+bc}}$ + $\displaystyle {\frac{ca}{c^5+a^5+ca}}$ $\displaystyle \leq$ 1.
Cuándo se cumple la igualdad?

Solución
Tenemos que:

a⁵ + b⁵ = (a + b)(a⁴ - a³b + a²b² - ab³ + b⁴)

= (a + b){(a - b)²(a² + ab + b²) + a²b²}

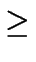$\displaystyle \geq$ a²b²(a + b)

y la igualdad se mantiene si y solo si a = b. Luego:

$\displaystyle {\frac{ab}{a^5+b^5+ab}}$ $\displaystyle \leq$ $\displaystyle {\frac{ab}{a^2b^2(a+b)+ab}}$

= $\displaystyle {\frac{1}{ab(a+b)+1}}$

= $\displaystyle {\frac{1}{ab(a+b+c)}}$

= $\displaystyle {\frac{c}{a+b+c}}$ .

Si se le asigna a X la suma 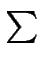$\sum$ ab/(a⁵+b⁵+ab), se obtiene:
X 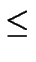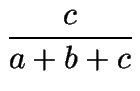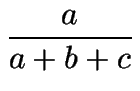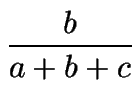$\displaystyle \leq$ $\displaystyle {\frac{c}{a+b+c}}$ + $\displaystyle {\frac{a}{a+b+c}}$ + $\displaystyle {\frac{b}{a+b+c}}$ = 1,
y la desigualdad queda establecida. La igualdad se cumple si y solo si a = b = c = 1.

1 2 3 4