|
Introducción
En el siglo diecisiete las series infinitas no eran muy conocidas,
pero a fines de ese siglo algunos matemáticos ya conocían
algunos teoremas generales sobre las mismas y la suma de una gran
cantidad de ellas.
Por ejemplo, la suma de la "serie telescópica''
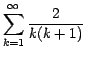 , la obtuvieron así: , la obtuvieron así:
Dunham menciona que el matemático Jacob Bernoulli "no solo probó la divergencia de la serie armónica, sino que
también conocía la suma exacta de un número de
[series] convergentes''3.
Por ejemplo, Jacob Bernoulli encontró la suma de la serie
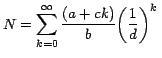 de la siguiente manera4: de la siguiente manera4:
Esto lo podemos escribir así:
Como cada serie entre paréntesis es una serie geométrica,
si suponemos que
Entonces
Es decir que
Dunham menciona también que Bernoulli encontró que:
y que
¿Cómo encontró Bernoulli esas sumas?. Esta pregunta me
motivó a investigar si había algún procedimiento,
parecido a los que usaban los matemáticos de aquella
época, que me permitiera encontrar fácilmente la suma de
ese tipo de series de potencias infinitas, a las que yo llamo "geométrico-polinomiales'', ya que son series geométricas
cuyos coeficientes están dados por una función polinomial
de grado 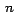 con coeficientes reales. con coeficientes reales.
Encontré un procedimiento cuya aplicación repetida
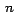 veces (igual al grado de la función polinomial), me
permitió convertir la serie infinita en una serie finita. El
resultado de esto lo pude expresar por medio de unas fórmulas
muy explícitas, que nos dan la serie finita que converge
exactamente al mismo valor que la serie infinita original. veces (igual al grado de la función polinomial), me
permitió convertir la serie infinita en una serie finita. El
resultado de esto lo pude expresar por medio de unas fórmulas
muy explícitas, que nos dan la serie finita que converge
exactamente al mismo valor que la serie infinita original.
A continuación explico, de una manera muy visual y muy
típica de la época de Bernoulli, como es este
procedimiento de reagrupamiento de los términos de la serie
infinita, que es la clave para poder simplificarla y convertirla
en una serie finita.
|
![\begin{displaymath}
\begin{array}{l}
\displaystyle{\sum_{k=1}^\infty { \frac{2}...
... \right)
+......} \right]=2\left[ 1 \right]=2} \\
\end{array}\end{displaymath}](img8.gif)
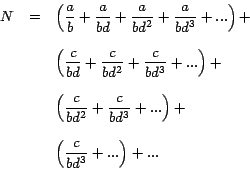
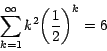
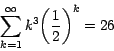
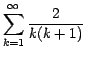 , la obtuvieron así:
, la obtuvieron así:
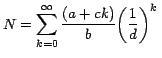 de la siguiente manera
de la siguiente manera