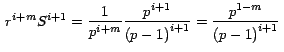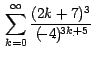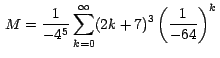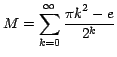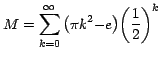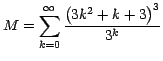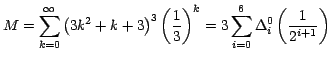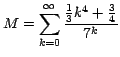|
Series geométrico-polinomiales
Llamaremos
Por lo tanto la ecuación (2) puede ser escrita así:
Esta manera tan visual de reagrupar los términos de una serie para luego obtener su suma, era muy usada en aquellos tiempos iniciales de la teoría de las series infinitas. Con métodos como ese los matemáticos de fines del siglo XVII empezaron a obtener el valor de muchas sumas infinitas. El resultado anterior lo formalizaremos ahora por medio del siguiente teorema:
Teorema 1
Si
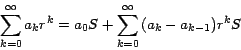
Demostración: Sabemos que la serie
Multiplicando ambos lados por
entonces
de donde
reagrupando los términos obtenemos:
Sea
entonces
Por el Teorema 1, esta serie la podemos escribir así:
Ahora a la suma que está entre corchetes le aplicamos
nuevamente el Teorema 1:
Nuevamente a la suma que está entre corchetes le aplicamos el
Teorema 1:
Ahora como la suma que está entre corchetes es la serie
geométrica S, obtenemos finalmente:
Vemos pues que la serie infinita (3) se redujo a la serie finita
(7) de solo 4 términos, luego que le aplicamos 3 veces
seguidas el Teorema 1.
Este resultado lo podemos expresar así:
La serie
Para esa función polinomial podemos crear la siguiente
Matriz de Diferencias Finitas:
Los coeficientes
Note que los coeficientes de la serie original (3) son los
coeficientes
Los coeficientes de la ecuación equivalente (4) están
dados por el coeficiente
Los coeficientes de la ecuación equivalente (5) están
dados por el coeficiente
Los coeficientes de la ecuación equivalente (6) están
dados por el coeficiente
Finalmente los coeficientes de la ecuación (7) están dados
por los coeficientes
Ahora demostraremos que en general, si la función
En la segunda mitad del siglo XIX el conocido matemático
George Boole demostró que si
La prueba es sencilla. Si
Entonces las primeras diferencias serán:
Similarmente obtenemos que las segundas diferencias serán de
la forma:
que es una función polinomial de grado
Y así sucesivamente hasta que finalmente las
donde
Para la demostración del caso general usaremos la siguiente
matriz de diferencias finitas:
Sea
Entonces
Por el Teorema 1 y siguiendo los mismos pasos que en el ejemplo
numérico anterior, esta serie la podemos escribir así:
Aplicando nuevamente el Teorema 1 a la parte que está entre
llaves obtenemos:
...............
El resultado anterior lo podemos formalizar por medio del siguiente teorema:
Teorema 2
Si 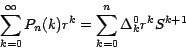
Demostración: Al aplicar el Teorema 1 por primera vez obtenemos que:
de donde obtenemos que
que podemos escribir así:
Similarmente, después de aplicar
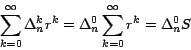
Sustituyendo este valor en la fórmula (*) obtenemos que:
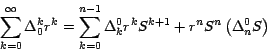
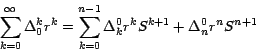
que podemos escribir así:
Con el Teorema 2 demostramos que si
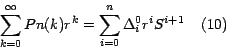
Como
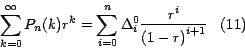
Ahora sea
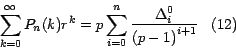
Asimismo teniendo en cuenta que
Entonces
Por lo tanto, también podemos escribir la fórmula (10)
así:
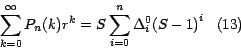
Supongamos ahora que queremos calcular la suma de la serie
mostrada en (3) pero a partir del tercer término, es decir a
partir del índice
Esto podemos escribirlo así:
El resultado final al aplicar la fórmula (10) resultará
ser la serie finita:
O sea que
Pero desde luego, es más fácil usar directamente la
columna 2 de la misma matriz que ya teníamos construida en la
Tabla 1 y resolverlo de la siguiente manera:
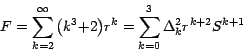
donde
Con esta fórmula obtenemos para
Veamos:
Teorema 3
Si
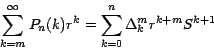
Demostración:
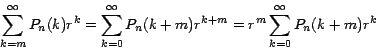
Por el Teorema 2 y denotando por
tenemos que:
Ahora, si
entonces:
ya que la columna 0 de la matriz
Por lo tanto podemos escribir la fórmula (*)
así:
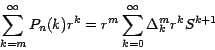
es decir que:
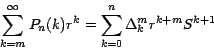
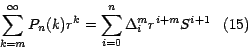
Como
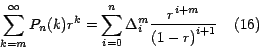
Ahora, teniendo en cuenta que
Por lo tanto, a la fórmula (15) la podemos escribir
también así:
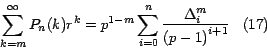
Similarmente, teniendo en cuenta que
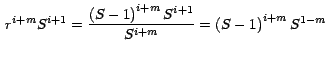
Por lo tanto, a la fórmula (15) la podemos escribir
también así:
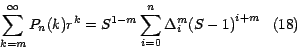
Estas últimas cuatro fórmulas contienen el resultado final
de mi investigación.
Veamos ahora algunos ejemplos del uso de estas fórmulas:
Ejemplo 1
Jacob Bernoulli encontró la suma de la serie
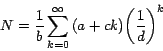
Usando nuestra fórmula podemos encontrar rápidamente la
suma de esa serie:
La matriz de diferencias finitas para la función
Por la fórmula (12) tenemos que:
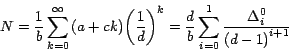
Por lo tanto:
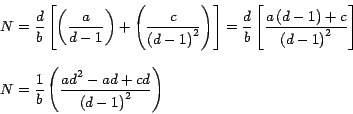
Ejemplo 2
Calcule la suma de la serie
Por la fórmula (12):
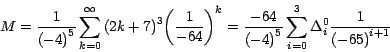
Es decir que:
![\begin{displaymath}
\begin{array}{l}
M=\displaystyle{\frac{-64}{-1024}\left[ {\...
...{48}{{65}^4 }} \right)} \right]=- 0.324146623} \\
\end{array}\end{displaymath}](img233.gif)
Ejemplo 3
Calcule la suma de la serie
Por la fórmula (12):
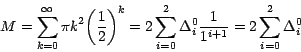
Es decir que:
![\begin{displaymath}
\begin{array}{l}
M=2 \left[ { - e+\pi +2\pi } \right] \\
\par
\\
\par
M=6\pi - 2e \,\approx \, 13.41299226\\
\end{array}\end{displaymath}](img250.gif)
Ejemplo 4
Calcule la suma de la serie
Tenemos que
Por la fórmula (12):
Es decir que:
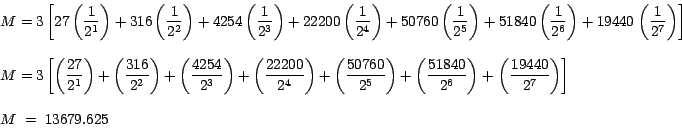
Ejemplo 5
Calcule la suma de la serie
La función
La matriz de diferencias finitas para la función
Por la fórmula (13) tenemos que:
![\begin{displaymath}
\begin{array}{l}
\displaystyle{ M=\sum_{k=0}^\infty { \frac...
...t)} \right] }\\
\par
\\
\par
{M\;=\;1.163065844}
\end{array}\end{displaymath}](img296.gif)
Ejemplo 6
Calcule la suma del ejercicio anterior pero sin incluir los
primeros 5 términos de la serie:
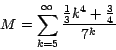
Usaremos la misma matriz de diferencias finitas del ejemplo
anterior.
Por la fórmula (18) tenemos que:
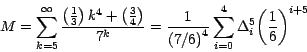
Por tanto, usaremos los coeficientes de la columna 5 de la Matriz de Diferencias Finitas de la Tabla E5:
Revista digital Matemática, Educación e Internet.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
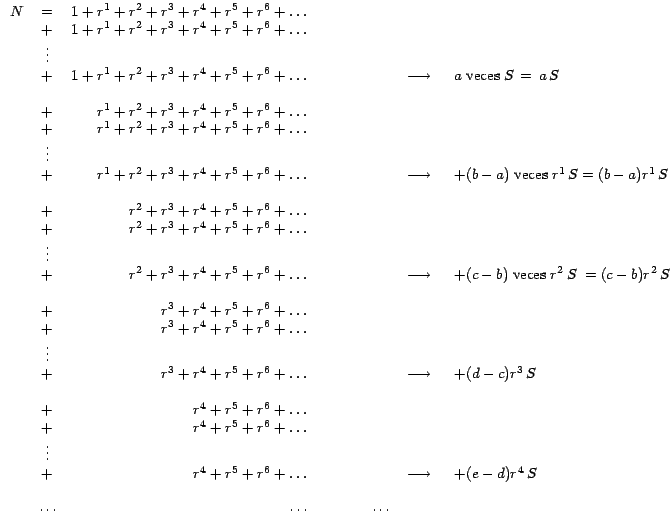
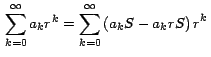
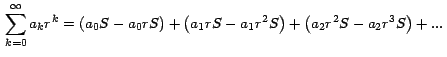
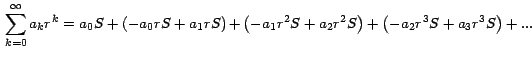
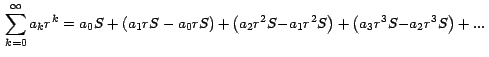
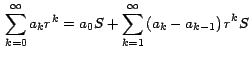
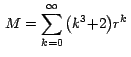
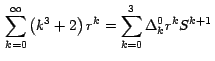
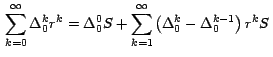
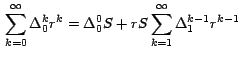
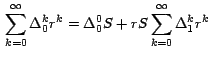
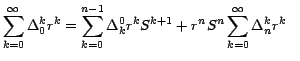 (*)
(*)
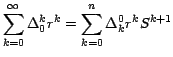
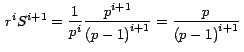
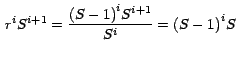
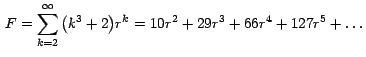
![$\, F = \displaystyle{\sum_{k=0}^\infty { \left[ {{\left( {k+2} \right)}^3 +2}
\...
...^2 \sum_{k=0}^\infty { \left[ {{\left(
{k+2} \right)}^3 +2} \right]} { r}^k }\,$](img176.gif)
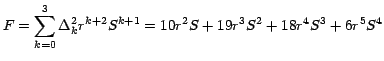
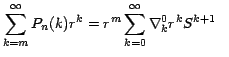 (*)
(*)