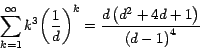|
En este artículo llamamos "series
geométrico-polinomiales'' a aquellas series geométricas
cuyos coeficientes están dados por una función polinomial
de grado n con coeficientes reales.
Toda serie de potencias infinita geométrico-polinomial, puede
convertirse en una serie de potencias finita de solo 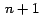 términos. Esto lo demostramos formalmente por medio del
Teorema 1 que nos muestra como expresar una serie
geométrica con relación a las diferencias finitas de sus
coeficientes y por medio del Teorema 2 que nos muestra
cómo, después de aplicar
términos. Esto lo demostramos formalmente por medio del
Teorema 1 que nos muestra como expresar una serie
geométrica con relación a las diferencias finitas de sus
coeficientes y por medio del Teorema 2 que nos muestra
cómo, después de aplicar 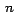 veces el Teorema 1,
llegamos a obtener una serie finita con solo veces el Teorema 1,
llegamos a obtener una serie finita con solo 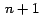 términos, equivalente a la serie infinita original. El
Teorema 3 nos permite encontrar cuál es la serie
finita equivalente a una serie infinita, cuyo valor inicial para
el índice es
términos, equivalente a la serie infinita original. El
Teorema 3 nos permite encontrar cuál es la serie
finita equivalente a una serie infinita, cuyo valor inicial para
el índice es 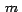 en vez de 0. en vez de 0.
En la revista Science del 24 de Junio de 2005 mencionan
que el profesor William Dunham, en su nuevo libro "The
Calculus Gallery, Masterpieces from Newton to Lebesgue''
proporciona la demostración de Jacob Bernoulli de la suma
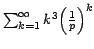 .
Originalmente la demostración apareció en la obra de Bernoulli "Tractatus de seriebus infinitis earumque summa finita" (Tratado
sobre las series infinitas y sus sumas finitas). .
Originalmente la demostración apareció en la obra de Bernoulli "Tractatus de seriebus infinitis earumque summa finita" (Tratado
sobre las series infinitas y sus sumas finitas).
Después de consultar el libro de Dunham encontramos que Bernoulli
dedujo que
usando un método muy similar al que vimos para la serie 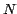 al
inicio de este artículo. al
inicio de este artículo.
Evidentemente Jacob Bernoulli encontró la suma de algunas series
infinitas geométrico-polinomiales, por métodos válidos para
algunos polinomios particulares, pero no por medio de un método
general, válido para cualquier polinomio, como si hicimos nosotros
y lo documentamos en este artículo.
Bibliografía
- Boole, G. 1960. A Treatise On The Calculus of Finite Differences.
Dover Publications, Inc. New York, United States of America.
(Republicación del trabajo original por Macmillan and Company
en 1872).
- Dunham, W. 1999. Euler The Master of Us All. The Mathematical
Association of America, United States of America.
- Dunham, W. 2005. The Calculus Gallery, Masterpieces from Newton to
Lebesgue. Princenton University Press, Princenton, NJ, United
States of America.
- Dunham, W. 1993. Viaje a través de los genios. Biografías
y teoremas de los grandes matemáticos. Ediciones Pirámide,
S.A., Madrid, España.
- Grabiner, J. V. 2005. Landmarks on the Road to Modern Analysis.
Revista Science, Vol 308, pp 1872. The American Association of
Science, US.
- Spiegel, M. 1971. Calculus of Finite Differences and Difference
Equations. Schaum's Outline Series. McGraw-Hill, Inc. (10th
printing, 1994), US.
Cidse
- Revista
virtual Matemática, Educación e Internet -
ITCR
Derechos Reservados
|