|
Software
|
Sea f una función continua con ecuación 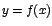 ,
definida en un intervalo ,
definida en un intervalo ![$[a,b]$](img2.gif) . .
La siguiente es la representación gráfica de f en el
intervalo ![$[a,b]$](img2.gif) . .
En la representación gráfica anterior puede observarse que la
función f es:
- Creciente en los intervalos
![$]a,x_{3}[$](img3.gif) , , ![$]x_{5},x_{6}[$](img4.gif)
- Decreciente en los intervalos
![$]x_{3},x_{5}[$](img5.gif) , , ![$]x_{6},b[$](img6.gif)
También se tiene que cuando la pendiente de la recta tangente es positiva, la función
f
crece; y cuando la pendiente de la recta
tangente es negativa, la función decrece.
Note además que en
los puntos
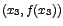 , ,
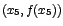 y y
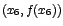 la recta tangente es horizontal, por lo que su
pendiente es cero, es decir, la primera
derivada de la función se anula en cada uno de esos puntos. la recta tangente es horizontal, por lo que su
pendiente es cero, es decir, la primera
derivada de la función se anula en cada uno de esos puntos.
En los siguientes teoremas se formalizan las apreciaciones anteriores.
Ejemplos:
- Determinemos los intervalos en que crece o decrece la
función con ecuación
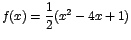 . .
Para ello calculemos la primera derivada de 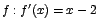 . .
Como
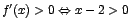 , o sea si , o sea si 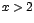 , entonces f es creciente para , entonces f es creciente para 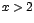 . .
Como
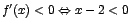 , o sea si , o sea si 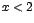 , entonces f es decreciente para , entonces f es decreciente para 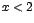 . .
En la representación gráfica de la función puede
observarse lo obtenido anteriormente.
- Determine en cuáles intervalos crece o decrece la
función con ecuación
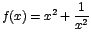 con con
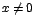 . .
La derivada de f está dada por
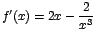 que
puede escribirse como que
puede escribirse como
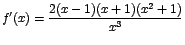
Como 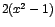 es positivo para toda x en es positivo para toda x en 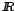 entonces: entonces:
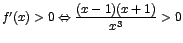 y y
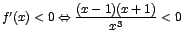
Para resolver estas desigualdades recurrimos a la siguiente tabla.
Luego: 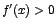 si si
![$x \in ]-1,0[ \; \cup \; ]1,+\infty[$](img27.gif) por lo
que la función f crece en el intervalo por lo
que la función f crece en el intervalo
![$]-1,0[ \; \cup \;
]1,+\infty[$](img28.gif) . .
Además: 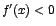 si si
![$x \in ]-\infty,-1[ \;
\cup \; ]0,1[$](img29.gif) de donde la función f decrece en el intervalo de donde la función f decrece en el intervalo
![$]-\infty,-1[ \; \cup \; ]0,1[$](img30.gif) . .
La representación gráfica de la función es la siguiente:
- Determinar los intervalos en que crece o decrece la
función f con ecuación
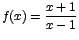 ,
con ,
con 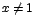 . .
La derivada de f es
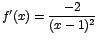 . .
Como 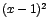 es mayor que cero para x en es mayor que cero para x en 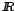 , , 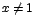 , y
además , y
además 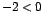 entonces entonces 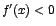 para todo x en para todo x en 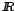 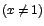 , por lo que la función f es decreciente para x en , por lo que la función f es decreciente para x en 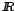 , ,
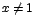 . La siguiente, es la representación gráfica de dicha
función: . La siguiente, es la representación gráfica de dicha
función:
Revista digital Matemática, Educación e Internet.
|