|
|
En el siguiente teorema se
establece cómo determinar los valores máximos y los valores
mínimos de una función, al estudiar los intervalos en que
crece o decrece la función.
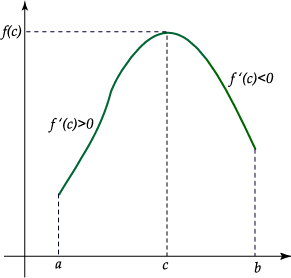
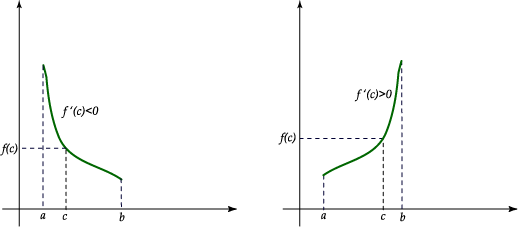
Las situaciones enunciadas en a., b. y c. pueden representarse
gráficamente como sigue:
Máximo relativo en 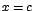
Mínimo relativo en 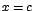
En 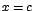 no hay ni máximo ni mínimo relativo. no hay ni máximo ni mínimo relativo.
En los siguientes ejemplos determinaremos los valores extremos de
una función cuya ecuación se da. Para ello, se calcula la
primera derivada de la función, luego se determinan los valores
críticos y por último se aplica el teorema anterior.
- 1.
-
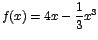
Note que f está definida para
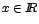
Como 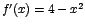 entonces entonces 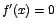 si y solo si si y solo si 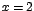 , ó , ó
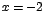 . .
Los valores críticos son 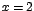 , y , x=-2. , y , x=-2.
Determinemos ahora cuándo 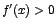 y cuándo y cuándo 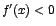 . .
Como
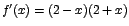 , se deben resolver las desigualdades: , se deben resolver las desigualdades:
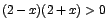 , , 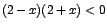 . Nos ayudamos con la tabla siguiente: . Nos ayudamos con la tabla siguiente:
Como 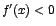 para para
![$x \in ]-\infty,-2[$](img102.gif) y y 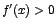 para para ![$x \in
[-2,2]$](img103.gif) entonces entonces 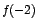 es un valor mínimo. es un valor mínimo.
Como 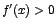 para para ![$x \in ]-2,2[$](img105.gif) y y 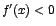 para para
![$x \in ]2,+\infty[$](img106.gif) entonces entonces 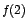 es un valor máximo. es un valor máximo.
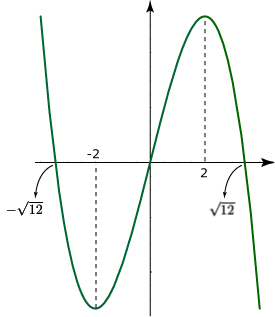
La representación gráfica de la función es la
siguiente:
Note que
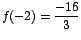 es un mínimo
relativo y que es un mínimo
relativo y que
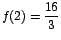 es un máximo
relativo, en el dominio de la función. es un máximo
relativo, en el dominio de la función.
- 2.
-
En este caso
![$f'(x)=\displaystyle\frac{(x+1)^2(11x-7)}{3\sqrt[3]{x-1}} $](img112.gif) (¡Compruébelo!) (¡Compruébelo!)
Luego, 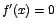 si y solo si si y solo si
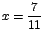 , ó, , ó, 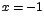
Además, 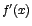 no existe si no existe si 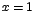 . .
Los valores críticos de f son
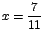 , , 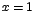 , , 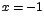 . .
Como 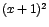 es positivo para todo es positivo para todo ![$x \in [-1,1]$](img111.gif) entonces para determinar cuando entonces para determinar cuando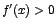 , y cuando , y cuando 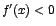 , basta con analizar la expresión , basta con analizar la expresión
![$\displaystyle\frac{11x-7}{\sqrt[3]{x-1}}$](img115.gif) . .
Utilizamos la siguiente tabla:
- i.
- Como
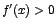 para para
![$x \in
\left]-1,\displaystyle\frac{11}{7}\right[$](img116.gif) y como f es continua
sobre ese intervalo, entonces y como f es continua
sobre ese intervalo, entonces 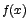 es creciente sobre es creciente sobre
![$\left]-1,\displaystyle\frac{11}{7}\right[$](img117.gif) por lo que por lo que
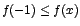 si si
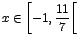 . .
Por lo tanto 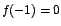 en un valor mínimo relativo de f. en un valor mínimo relativo de f.
- ii.
- Como
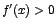 para para
![$x \in
\left]-1,\displaystyle\frac{11}{7}\right[$](img116.gif) y y 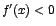 para para
![$x\in
\left]\displaystyle\frac{11}{7},1\right[$](img121.gif) , entonces , entonces
![$f\left(\displaystyle\frac{1}{7}\right)=\sqrt[3]{\displaystyle\frac{16}{49}}$](img122.gif) . .
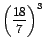 es un valor máximo
relativo de f. es un valor máximo
relativo de f.
- iii.
- Como
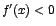 si si
![$x\in
\left]\displaystyle\frac{11}{7},1\right[$](img121.gif) y como f es continua
sobre y como f es continua
sobre
![$\left]\displaystyle\frac{11}{7},1\right]$](img124.gif) entonces f es
decreciente sobre entonces f es
decreciente sobre
![$\left]\displaystyle\frac{11}{7},1\right]$](img124.gif) , y
por tanto , y
por tanto 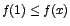 cuando cuando
![$x \in
\left]\displaystyle\frac{11}{7},1\right]$](img126.gif) . Luego . Luego 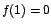 es un
valor mínimo relativo de f. es un
valor mínimo relativo de f.
- 3.
-
,
![$x \in
[-2,2]$](img103.gif)
Se tiene que
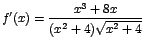 (¡Compruébelo!) (¡Compruébelo!)
Ahora, 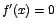 si y solo si si y solo si 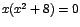 es decir, si es decir, si 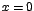 . .
Los valores críticos de f son 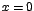 , , 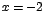 , , 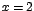 , estos
últimos por ser extremos del intervalo. , estos
últimos por ser extremos del intervalo.
Como
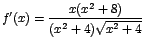 ,
y, ,
y, 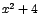 , , 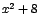 , y, , y, 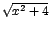 son expresiones positivas
para todo son expresiones positivas
para todo
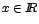 entonces el signo de entonces el signo de 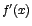 estará determinado por
la variación de x. estará determinado por
la variación de x.
Luego se tiene:
-
- i.
- Como
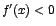 para para ![$x \in ]-2,0]$](img135.gif) y f es continua en y f es continua en
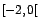 entonces f es decreciente sobre entonces f es decreciente sobre 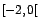 . Luego . Luego
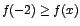 para para 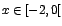 , y , y
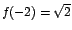 es un
máximo relativo de f. es un
máximo relativo de f.
- ii.
- Como
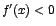 para para ![$x \in
]-2,0[$](img140.gif) y y 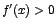 para para ![$x \in ]0,2[$](img141.gif) , entonces , entonces 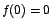 es un
mínimo relativo de f. es un
mínimo relativo de f.
- iii.
- Como
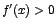 para para ![$x\in ]0,2]$](img143.gif) y f es continua en y f es continua en
![$]0,2]$](img144.gif) entonces f es creciente en entonces f es creciente en ![$]0,2]$](img144.gif) . Luego . Luego 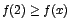 para
para ![$x\in ]0,2]$](img143.gif) y y 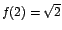 es un máximo relativo de f. es un máximo relativo de f.
Ejercicio:
Hacer un estudio similar para:
Revista digital Matemática, Educación e Internet.
|
![]()
![]() para
para
![]() y
y ![]() para
para ![]() entonces
entonces ![]() es un valor mínimo.
es un valor mínimo.
![]() para
para ![]() y
y ![]() para
para
![]() entonces
entonces ![]() es un valor máximo.
es un valor máximo.