|
|
Si f es una función dada, entonces 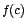 es un valor máximo relativo de f, si existe un intervalo
abierto es un valor máximo relativo de f, si existe un intervalo
abierto ![$]a,b[$](img10.gif) tal que tal que 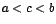 y y 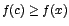 para para ![$x \in
]a,b[$](img40.gif) , siendo x un valor del dominio de la función. , siendo x un valor del dominio de la función.
Si 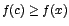 para toda x en el dominio de f, entonces para toda x en el dominio de f, entonces
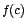 es el valor máximo de f o
máximo absoluto. es el valor máximo de f o
máximo absoluto.
Similarmente, 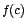 es un valor mínimo
relativo de la función f, si existe un intervalo abierto es un valor mínimo
relativo de la función f, si existe un intervalo abierto
![$]a,b[$](img10.gif) tal que tal que 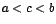 y y 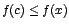 para para ![$x \in
]a,b[$](img40.gif) ,
con x en el dominio de f. ,
con x en el dominio de f.
Si
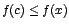 para toda x en el dominio de f, entonces se dice que para toda x en el dominio de f, entonces se dice que
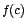 es el valor mínimo de dicha función. También se
llama mínimo absoluto. es el valor mínimo de dicha función. También se
llama mínimo absoluto.
Ejemplo:
Considere una función f definida en un intervalo ![$]c,d[$](img42.gif) , cuya
representación gráfica es la siguiente: , cuya
representación gráfica es la siguiente:
Note que 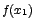 , es un máximo relativo y , es un máximo relativo y 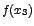 es el
máximo valor que toma la función en el intervalo en que
está definida. es el
máximo valor que toma la función en el intervalo en que
está definida.
Similarmente, 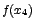 es un valor mínimo relativo y es un valor mínimo relativo y
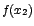 es el mínimo absoluto de la función en es el mínimo absoluto de la función en ![$]c,d[$](img42.gif) . .
|
|
Teorema
2 |
|
Sea c un punto interior del dominio de una función f.
Si 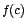 es un valor máximo relativo de f y si existe es un valor máximo relativo de f y si existe 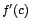 entonces
entonces 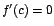 . .
Prueba: al final del capítulo.
|
Ejemplo:
|
Considere la función f definida por
|
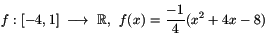 |
Su representación gráfica es la siguiente:
Puede observarse que cuando x toma el valor de 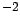 entonces la
función tiene un valor máximo. En este caso entonces la
función tiene un valor máximo. En este caso 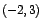 es
precisamente el vértice de la parábola con ecuación: es
precisamente el vértice de la parábola con ecuación:
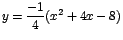 . .
Según el teorema anterior debe cumplirse que 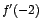 es igual a
cero. es igual a
cero.
En efecto, como
 , al sustituir x por
-2 se obtiene que , al sustituir x por
-2 se obtiene que
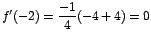 , que
era lo que quería comprobarse. , que
era lo que quería comprobarse.
|
|
Teorema
3
|
|
Sea c un punto interior del dominio de una función f. Si 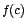 es un valor mínimo relativo de f y si
es un valor mínimo relativo de f y si 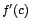 existe, entonces existe, entonces
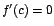 . .
La demostración es similar a la del teorema anterior.
|
Ejemplo:
| Considere la función f definida por: |
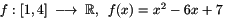 |
Su representación gráfica es la siguiente:
Note que la función f tiene un valor mínimo en
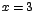 dado por dado por 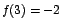 . El punto . El punto 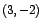 es el vértice de la
parábola con ecuación es el vértice de la
parábola con ecuación 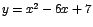 . .
De acuerdo con el teorema 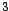 debe cumplirse que debe cumplirse que 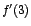 sea
igual a cero. sea
igual a cero.
Como 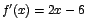 entonces entonces
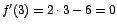 y se verifica lo
enunciado respecto al valor mínimo. y se verifica lo
enunciado respecto al valor mínimo.
Observación:
El recíproco de los dos teoremas
anteriores no es cierto. Es decir, el hecho de que
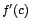 sea igual a cero, no implica que en sea igual a cero, no implica que en 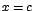 exista un máximo o un mínimo.
exista un máximo o un mínimo.
Por ejemplo, para la función f con ecuación 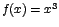 , se
tiene que , se
tiene que 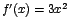 , y , y 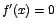 si si 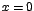 ; sin embargo, en ; sin embargo, en
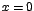 no hay ni un valor máximo ni un valor mínimo, como puede
observarse en la siguiente representación gráfica de la
función. no hay ni un valor máximo ni un valor mínimo, como puede
observarse en la siguiente representación gráfica de la
función.
|
|
Definición
|
|
|
Sea f una función. Recibe el nombre de
valores críticos del dominio de f, aquellos en los
que
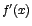 es igual a cero o en los que es igual a cero o en los que
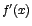 no existe. no existe.
|
Ejemplo:
Determinemos los valores críticos de las funciones con ecuaciones:
-
-
-
Solución:
- a.
- Como
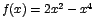 , entonces , entonces 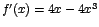
Ahora: 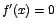 si y solo si si y solo si 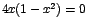 o sea si o sea si 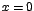 , ó, , ó, 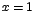 , ó, , ó, 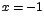
Luego, los valores críticos de f son: x=0, x=1, y x=-1.
- b.
- Como
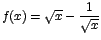 entonces
entonces
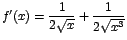
Luego
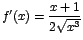 , de donde , de donde 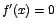 si y
solo si si y
solo si 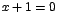 , o sea, si , o sea, si 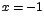
Por lo tanto el valor crítico de f es 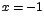 . .
Note que aunque 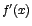 se indefine en se indefine en 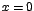 , como este valor no
pertenece al dominio de f, entonces no es valor crítico de dicha
función. , como este valor no
pertenece al dominio de f, entonces no es valor crítico de dicha
función.
Observación:
Reciben el nombre de valores extremos de una función f los valores
máximos relativos y los valores mínimos relativos de f. Dada
una función f cuyo dominio es el intervalo k, un valor 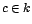 será un valor crítico de x para la función
f si:
será un valor crítico de x para la función
f si:
| a. |
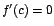 ó ó |
| b. |
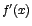 no existe ó no existe ó |
- c.
|
c es un extremo del intervalo k. |
En este último caso, si ![$k=[a,b]$](img87.gif) entonces "a" y "b" son valores
críticos. Si entonces "a" y "b" son valores
críticos. Si 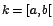 o si o si 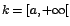 entonces "a" es un
valor crítico. Si entonces "a" es un
valor crítico. Si ![$k=]a,b[$](img90.gif) , o si , o si ![$k=]-\infty,b]$](img91.gif) entonces "b"
es un valor crítico. Si entonces "b"
es un valor crítico. Si ![$k=]a,b[$](img90.gif) , entonces ni "a" ni "b" son
valores críticos (note que los valores extremos de un intervalo
abierto no son elementos del intervalo). , entonces ni "a" ni "b" son
valores críticos (note que los valores extremos de un intervalo
abierto no son elementos del intervalo).
Revista digital Matemática, Educación e Internet.
|