Lic. Elsie Hernández S.

  1 2 3 4 5 6 7 8 9

 

 

 

Criterio de la segunda derivada para establecer los valores máximos y
los valores mínimos de una función

Además de proporcionar información sobre la concavidad de la gráfica de una función, la segunda derivada permite establecer si un punto crítico es un valor máximo o un valor mínimo.

El siguiente teorema se refiere a este segundo aspecto.

 

  Teorema
 

Sea f una función con dominio D.

Si $f'(x)$ está definida para $x \in ]a,b[$ donde $]a,b[ \subset D$ y si $f'(x_{0})=0$ con $x_{0} \in ]a,b[$ entonces:

a.

 

 $f(x_{0})$ es un valor máximo relativo de f si se cumple que $f''(x_{0})<0$
b. $f(x_{0})$ es un valor mínimo relativo de f si se cumple que $f''(x_{0})>0$
 

Demostración: Al final del capítulo.

 

Ejemplos:

Utilizando el teorema anterior vamos a determinar los valores máximos y los valores mínimos de las funciones cuyas ecuaciones son:

 

1.    $f(x)=\displaystyle\frac{x^2}{x+1}$, $x \in ]-4,2[$

Note que la función f no está definida en $x=-1$

La derivada de f está dada por $f'(x)=\displaystyle\frac{x(x+2)}{(x+1)^2}$, $x \neq -1$

Los valores críticos de f se obtienen cuando $f'(x)=0$. En este caso, $f'(x)=0$ si y solo si $x=0$, ó $x=-2$.

Ahora, la segunda derivada de f es $f''(x)=\displaystyle\frac{2}{(x+1)^3}$

Vamos a evaluar $f''(x)$ en $x=0$ y en $x=-2$

 

a. $f''(0)=2$; como $2 > 0$ entonces $f(0)$ es un valor mínimo relativo de f.

 
b.

 

 $f''(-2)=-2$; como $-2<0$ entonces $f(-2)$ es un valor máximo relativo de f.

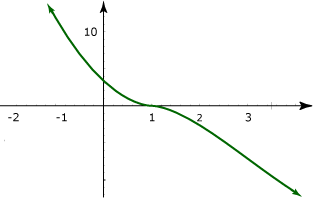
Gráficamente se tiene en el intervalo $]-4,2[$


2.

Se tiene que $D_{g} = I \! \! R$

La primera derivada de g está dada por  

 

Como $g'(x)=0$ cuando $x=1$ y cuando $x=6$ entonces estos son los valores críticos de g.

La segunda derivada de g es $g''(x)=\displaystyle\frac{5(x-3)}{3\sqrt[3]{x-1}}$

Evaluando $g''(x)$ en $x=6$ se tiene que  

 que es mayor que cero, por lo que $g(6)$ es un valor mínimo relativo de g.

Observe que $g''$ no puede evaluarse en $x=1$ pues hace cero el denominador por lo que para este valor crítico debe utilizarse el criterio de la primera derivada.

Analizando $g'(x)=(x-1)^\frac{2}{3} (x-6)$ se obtiene que $g'(x)<0$ para $x \in ]-\infty,1[$ y $g'(x)<0$ para $x \in ]1,6[$ por lo que al no existir cambio de signo resulta que $f(1)$ no es ni máximo ni mínimo. El gráfico de g se muestra a continuación.

Inicio
Revista digital Matemática, Educación e Internet.