Para dibujar curvas en el espacio debemos parametrizar su ecuación.
Así
-
C : f (x, y) = 0parametrizada tiene la forma
C : (x(t), y(t), 0) t
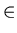 [a, b].
[a, b].
Plano xy
-
C : f (y, z) = 0parametrizada tiene la forma
C : (0, y(t), z(t)) t
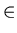 [a, b].
[a, b].
plano yz
-
C : f (x, z) = 0parametrizada tiene la forma
C : (x(t), y(t), 0) t
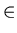 [a, b].
plano xz.
[a, b].
plano xz.
Ejemplos de curvas parametrizadas.
- Segmento de recta de A(a,b) a B(c,d)
[a + t(c - a), b + t(d - b), 0] t
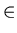 [0, 1]
[0, 1]
- Círculo:
(x - h)2 + (y - k)2 = r2
[h + r cos t, k + r sin t, 0] t
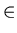 [0,
[0,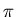 ]
]
- Elipse:
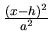 +
+ 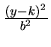 [h + a cos t, k + b sin t, 0] t
[h + a cos t, k + b sin t, 0] t 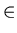 [0, 2
[0, 2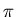 ]
]
- Hipérbola:
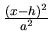 -
- 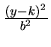 [h
[h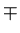 a
a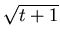 , k
, k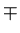 b
b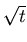 , 0] t
, 0] t 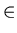 [- a, a]
a cualquier número positivo con las 4 posibilidades de signo.
[- a, a]
a cualquier número positivo con las 4 posibilidades de signo.
- Una parametrización se puede también obtener despejando una variable y tomándola como parámetro.
Ejemplo
La hipérbola
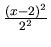 -
- 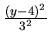 parametrizada es
parametrizada es
[2±2
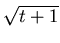
, 4±| 3
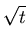
,
o]
t 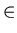
[- 2, 2]
Revista
1
2
3
4 5
6
7 8
9
10
11
12 13
|
Revista Matemáticas,
Educación e Internetâ
Derechos Reservados |
![]() -
- ![]() parametrizada es
parametrizada es