En

En ([2]) se calcula tan $\left(\vphantom{ 1 \displaystyle{1\over 2} }\right.$ 1 $\displaystyle {1\over 2}$ $\left.\vphantom{ 1 \displaystyle{1\over 2} }\right)^{o}_{}$ , fórmula que reproducimos a continuación:

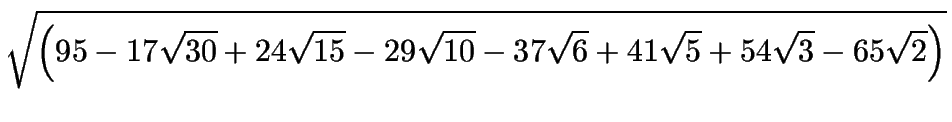tan $\left(\vphantom{ 1 \displaystyle{1\over 2} }\right.$ 1 $\displaystyle {1\over 2}$ $\left.\vphantom{ 1 \displaystyle{1\over 2} }\right)^{o}_{}$ = $\displaystyle {1\over \sqrt{2}}$ $\displaystyle \sqrt{\left( 95-17 \sqrt{30}+24 \sqrt{15}-29\sqrt{10}-37 \sqrt{6}+41\sqrt{5}+54\sqrt{3}-65\sqrt{2}\right)}$

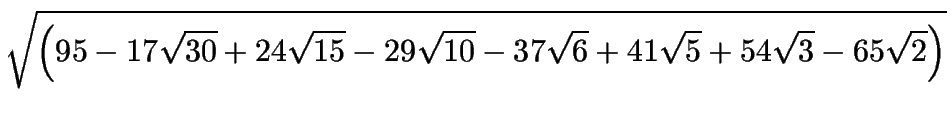- $\displaystyle {1\over \sqrt{2}}$ $\displaystyle \sqrt{\left( 95-17 \sqrt{30}+24 \sqrt{15}-27\sqrt{10}-35 \sqrt{6}+39\sqrt{5}+50\sqrt{3}-65\sqrt{2}\right)}$

2.Cálculo de las funciones seno y coseno de 15^o

En algunos manuales aparecen los valores de estas funciones, para nuestra comodidad las calcularemos aquí.
Utilizando las fórmulas del ángulo medio tenemos:

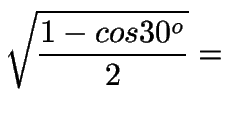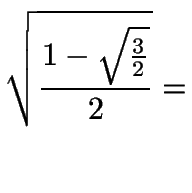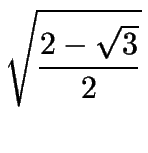sen15^o =	$\displaystyle {\sqrt{1-cos 30^o\over 2}=}$	$\displaystyle {\sqrt{1-\sqrt{3\over 2}\over2}=}$	$\displaystyle {\sqrt{2-\sqrt{3}\over 2}}$
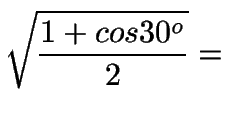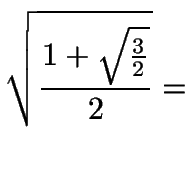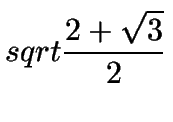cos15^o =	$\displaystyle {\sqrt{1+cos 30^o\over 2}=}$	$\displaystyle {\sqrt{1+\sqrt{3\over 2}\over2}=}$	$\displaystyle {sqrt{2+\sqrt{3}\over 2}}$

Las expresiones $\sqrt{2-\sqrt{3}}$ y $\sqrt{2+\sqrt{3}}$ pueden simplificarse con ayuda de las fórmulas:

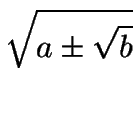$\displaystyle \sqrt{a\pm\sqrt{b}}$

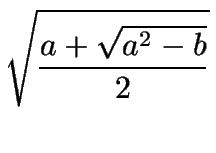$\displaystyle {\sqrt{a+\sqrt{a^2-b}\over 2}}$

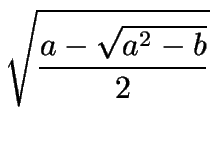$\displaystyle {\sqrt{a-\sqrt{a^2-b}\over 2}}$

Así tenemos:

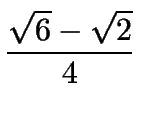sen15^o	=	$\displaystyle {\sqrt{6}-\sqrt{2}\over4}$
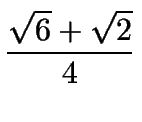cos15^o	=	$\displaystyle {\sqrt{6}+\sqrt{2}\over4}$