4.Cálculo de las funciones seno y coseno de los ángulos de 24o,12o,6o,3o
Tenemos que
54o - 30o = 24o, así:
| sen24o | = |
sen |
| = | sen 54o cos 30o - cos 54o sen 30o | |
| = |
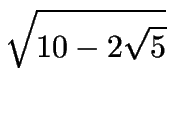 |
|
| cos 24o | = | cos 54o cos 30o + sen 54o sen 30o |
| = |
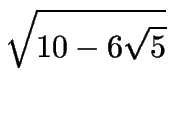 |
|
| sen 12o | = |
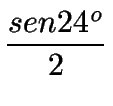 |
| = |
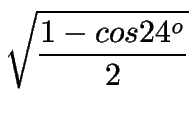 |
|
| = |
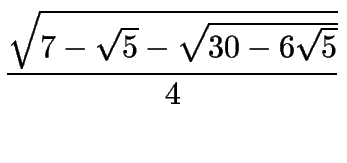 |
|
| cos12o | = |
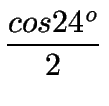 |
| = |
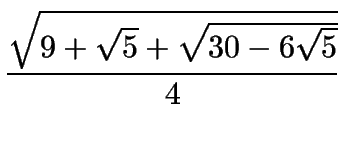 |
También se tiene que
6o = 36o - 30o y entonces :
| sen 6o | = | sen 36o cos 30o - cos 36o sen 30o |
| = |
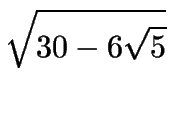 - - |
|
| cos 6o | = | cos 36o cos 30o - sen 36o sen 30o |
| = |
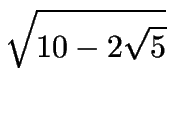 + + |
Con las fórmulas del ángulo medio se obtiene:
| sen 3o | = |
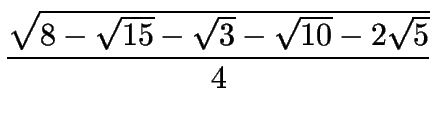 |
| cos 3o | = |
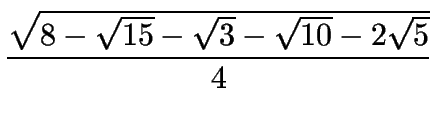 |