5

5.Cálculo de las funciones seno y coseno de ángulo con medidas de 21^o, 33^o, 39^o ó 42^o.

Utilizando las relaciones:

21^o	=	36^o	-	15^o
33^o	=	36^o	-	3^o
39^o	=	54^o	-	15^o
42^o	=	60^o	-	18^o

Calculamos:

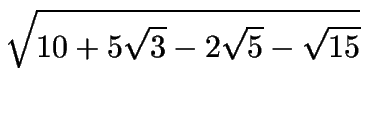sen 21^o	=	$\displaystyle {\sqrt{2}\over16}$ $\displaystyle \left[\vphantom{2\sqrt{10+5\sqrt{3}-2\sqrt{5}-\sqrt{15}}-\sqrt{15}+\sqrt{5}-\sqrt{3}+1}\right.$ 2 $\displaystyle \sqrt{10+5\sqrt{3}-2\sqrt{5}-\sqrt{15}}$ - $\displaystyle \sqrt{15}$ + $\displaystyle \sqrt{5}$ - $\displaystyle \sqrt{3}$ + 1 $\displaystyle \left.\vphantom{2\sqrt{10+5\sqrt{3}-2\sqrt{5}-\sqrt{15}}-\sqrt{15}+\sqrt{5}-\sqrt{3}+1}\right]$

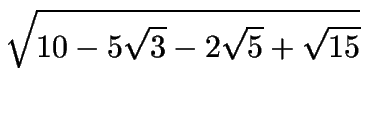cos 21^o	=	$\displaystyle {\sqrt{2}\over16}$ $\displaystyle \left[\vphantom{2\sqrt{10-5\sqrt{3}-2\sqrt{5}+\sqrt{15}}+\sqrt{15}+\sqrt{5}+\sqrt{3}+1}\right.$ 2 $\displaystyle \sqrt{10-5\sqrt{3}-2\sqrt{5}+\sqrt{15}}$ + $\displaystyle \sqrt{15}$ + $\displaystyle \sqrt{5}$ + $\displaystyle \sqrt{3}$ + 1 $\displaystyle \left.\vphantom{2\sqrt{10-5\sqrt{3}-2\sqrt{5}+\sqrt{15}}+\sqrt{15}+\sqrt{5}+\sqrt{3}+1}\right]$

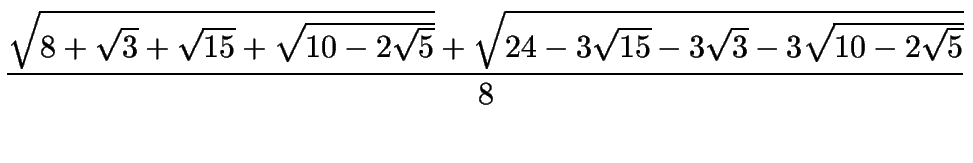sen 33^o	=	$\displaystyle {\sqrt{8+\sqrt{3}+\sqrt{15}+\sqrt{10-2\sqrt{5}}}+\sqrt{24-3\sqrt{15}-3\sqrt{3}-3\sqrt{10-2\sqrt{5}}}\over8}$

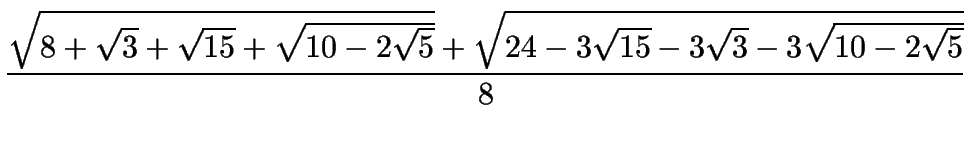cos 33^o	=	$\displaystyle {\sqrt{24+3\sqrt{15}+3\sqrt{3}+3\sqrt{10-2\sqrt{5}}}-\sqrt{8-\sqrt{15}-\sqrt{3}-\sqrt{10-2\sqrt{5}}}\over8}$

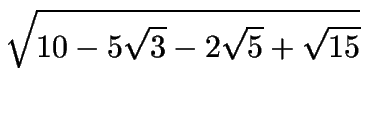sen 39^o	=	$\displaystyle {\sqrt{2}\over16}$ $\displaystyle \left[\vphantom{\sqrt{15}+\sqrt{5}+\sqrt{3}+1-2\sqrt{10-5\sqrt{3}-2\sqrt{5}+\sqrt{15}}}\right.$ $\displaystyle \sqrt{15}$ + $\displaystyle \sqrt{5}$ + $\displaystyle \sqrt{3}$ + 1 - 2 $\displaystyle \sqrt{10-5\sqrt{3}-2\sqrt{5}+\sqrt{15}}$ $\displaystyle \left.\vphantom{\sqrt{15}+\sqrt{5}+\sqrt{3}+1-2\sqrt{10-5\sqrt{3}-2\sqrt{5}+\sqrt{15}}}\right]$

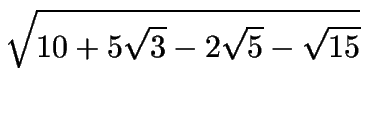cos 39^o	=	$\displaystyle {\sqrt{2}\over16}$ $\displaystyle \left[\vphantom{2\sqrt{10+5\sqrt{3}-2\sqrt{5}-\sqrt{15}}+\sqrt{15}-\sqrt{5}+\sqrt{3}-1}\right.$ 2 $\displaystyle \sqrt{10+5\sqrt{3}-2\sqrt{5}-\sqrt{15}}$ + $\displaystyle \sqrt{15}$ - $\displaystyle \sqrt{5}$ + $\displaystyle \sqrt{3}$ - 1 $\displaystyle \left.\vphantom{2\sqrt{10+5\sqrt{3}-2\sqrt{5}-\sqrt{15}}+\sqrt{15}-\sqrt{5}+\sqrt{3}-1}\right]$

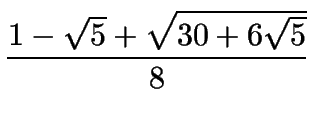sen 42^o	=	$\displaystyle {1-\sqrt{5}+\sqrt{30+6\sqrt{5}}\over 8}$

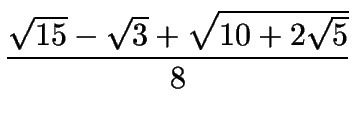cos 42^o	=	$\displaystyle {\sqrt{15}-\sqrt{3}+\sqrt{10+2\sqrt{5}}\over 8}$