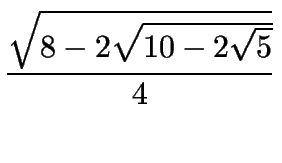3

3.Cálculo de las funciones seno y coseno de 36^o,18^o,27^o,9^o

Para calcular estas funciones trigonométricas de 36^o se utiliza un triángulo isósceles como el que se ilustra en la figura:

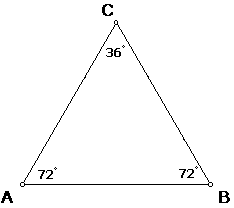
Se observa que este triángulo tiene una propiedad muy particular, la cual es que al trazar la bisectriz de uno de los ángulos de 72^o, por ejemplo B, se forman dos triángulos isósceles, así como se ilustra en la figura que sigue:

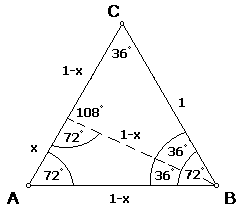
En la figura se trazó la bisectriz del ángulo B. Aplicando el teorema de la bisectriz se obtiene:

$\displaystyle {x\over 1-x}$

$\displaystyle {1-x\over x}$

Así se deduce que:

1-x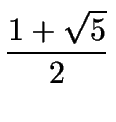

$\displaystyle {1+\sqrt{5}\over 2}$

Si en el triángulo anterior trazamos también la bisectriz del ángulo de 108^o obtenemos los datos siguientes:

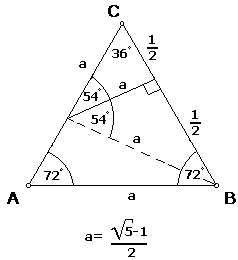
De la figura anterior se deduce:

sen 36^o = 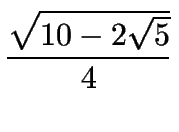$\displaystyle {\sqrt{10-2\sqrt{5}}\over 4}$

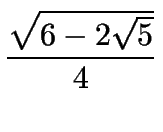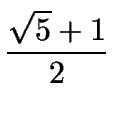
cos 36^o = $\displaystyle {\sqrt{6-2\sqrt{5}}\over 4}$ = $\displaystyle {\sqrt{5}+1\over 2}$

sen 54^o = 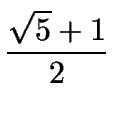$\displaystyle {\sqrt{5}+1\over 2}$

cos 54^o = 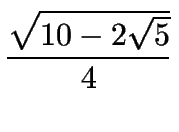$\displaystyle {\sqrt{10-2\sqrt{5}}\over 4}$

Utilizando las fórmulas del ángulo medio calculamos:

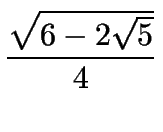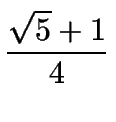
sen 18^o = $\displaystyle {\sqrt{6-2\sqrt{5}}\over 4}$ = $\displaystyle {\sqrt{5}+1\over 4}$

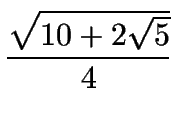
cos 18^o = $\displaystyle {\sqrt{10+2\sqrt{5}}\over 4}$

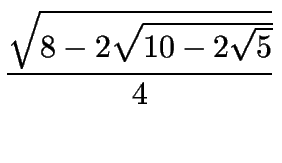
sen 27^o = $\displaystyle {\sqrt{8-2\sqrt{10-2\sqrt{5}}}\over 4}$

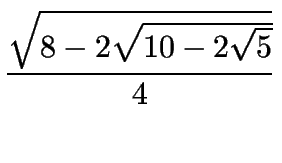
cos 27^o = $\displaystyle {\sqrt{8+2\sqrt{10-2\sqrt{5}}}\over 4}$

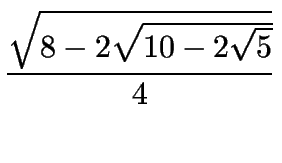
sen 9^o = $\displaystyle {\sqrt{8-2\sqrt{10+2\sqrt{5}}}\over 4}$

cos 9^o = $\displaystyle {\sqrt{8+2\sqrt{10+2\sqrt{5}}}\over 4}$