Graficando con Excel

| G.Figueroa M. | Revista Digital Matemática, Educación e Internet |

 

1 2  3  4  5  6 7   8

Graficando curvas polares

La gráfica de una ecuación polar $r = f(\theta)$ puede verse como un caso particular de una curva paramétrica en cual el parámetro $t=\theta$, $x=rCos(\theta)$, $y=r Sen(\theta)$ y $r = f(\theta)$, es decir

$$\left \{ \begin{array}{lclr} x & = & f(\theta) Cos(\theta) &... ...a,b] \\ y & = & f(\theta)Sen(\theta) & \\ \end{array}\right.$$

Habiendo observado esto, el problema de trazar la gráfica de una ecuación polar se resuelve con el mismo procedimiento que hemos estado utilizando.

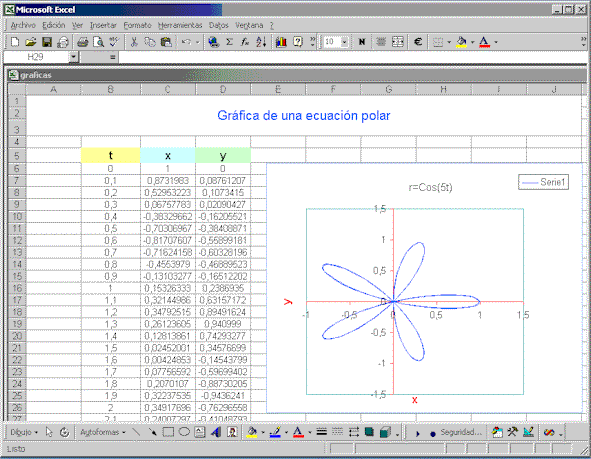
Como ejemplo, para trazar la gráfica de la ecuación $r=Cos(5 \theta)$ procedemos de la siguiente forma:

1. En la celda B6 escribimos 0.

2. En la celda B7 escribimos =B6 + 0,1 y generamos los valores del paramétro hasta $2 \pi$, aproximadamente.

3. En la celda C6 escribimos la fórmula para las coordenadas $x$: =Cos(5*B6)Cos(b6) y las generamos.

4. En la celda D6 escribimos la fórmula para las coordenadas $y$: =Cos(5*B6)Sen(b6) y las generamos.

5. Y con la ayuda del asistente trazamos el gráfico (figura 8). Recuerde que el gráfico es de tipo $xy$ de dispersión con líneas suavizadas y sin marcadores de datos.

 

Figura 8: Gráfica de la ecuación polar

 

1 2  3  4  5  6 7   8

 

Revista digital Matemática, Educación e Internet.
Derechos Reservados