|
Preliminares: Tópicos Elementales de la Teoría de
Números.
Definiciones y resultados básicos
Seguidamente se presentarán algunas definiciones y resultados
elementales de la Teoría de Números, que permitirán
posteriormente la introducción de los métodos de
factorización.
Definición 1
Dado dos números naturales  y
y 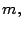 se dice que
se dice que  es un factor
o divisor de
es un factor
o divisor de  si existe un número natural
si existe un número natural 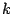 tal que:
tal que: 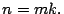 Se dice
que
Se dice
que  es un múltiplo de
es un múltiplo de  y de
y de 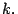
- Ejemplo 1.
-
- El número 4 es divisor de
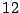 pues
pues
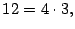 en este caso se toma k igual a
en este caso se toma k igual a
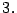
A continuación se enumeran algunos resultados consecuencia de la primer
definición

- Grupo de Resultados A
- Si
 es factor de
es factor de  entonces
entonces
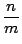 es factor de
es factor de 
- Para todo número natural
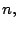 se tiene que
se tiene que 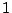 y
y  son divisores
de
son divisores
de 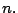
- Si
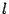 es divisor de
es divisor de  y
y  es divisor de
es divisor de  entonces
entonces 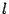 es divisor
es divisor

- Justificación de los resultados A.
- Si
 es un factor de
es un factor de  entonces existe
entonces existe
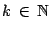 tal que
tal que 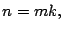 por lo que
por lo que
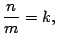 y en consecuencia
y en consecuencia 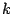 es un factor de
es un factor de  , pues
, pues 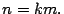 Este resultado señala que si
Este resultado señala que si
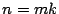 entonces tanto
entonces tanto  como
como 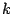 son factores de
son factores de 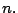
- Dado que
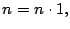 entonces por el resultado anterior,
entonces por el resultado anterior,  y
y 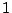 son
divisores de
son
divisores de 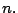
- Se tiene que existen dos naturales,
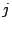 y
y 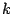 que cumplen:
que cumplen: 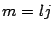 y
y
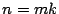 entonces
entonces
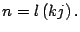 Por lo tanto
Por lo tanto 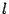 es divisor de
es divisor de 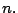
Se entenderá por factorizar un número  como el proceso mediante el
cual se expresa
como el proceso mediante el
cual se expresa  como una multiplicación de dos o más factores
diferentes de
como una multiplicación de dos o más factores
diferentes de 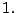
- Ejemplo 2.
-
- Las posibles factorizaciones de
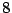 son:
son:
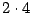 y
y
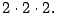
Definición 2.
Se define A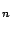 como el conjunto de divisores de
como el conjunto de divisores de
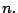
- Ejemplo 3.
-
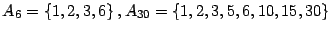
A continuación se enumeran algunos propiedades del conjunto 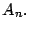
- Grupo de Resultados B.
- Para todo
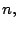
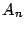 no es vacío
no es vacío
- Si
 es divisor de
es divisor de  entonces
entonces
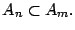
- El máximo elemento de
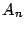 es
es 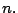
- Para cualesquiera números naturales
 y
y 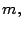 se tiene que
se tiene que
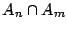 es diferente del conjunto
es diferente del conjunto
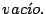
- Justificación de los resultados B.
- Por el resultado
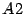 se tiene que
se tiene que
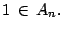 Además
Además
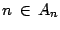
- Sea
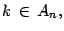 entonces
entonces 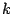 es divisor de
es divisor de  y
como
y
como  es divisor de
es divisor de  , por el resultado
, por el resultado 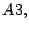 se tiene que
se tiene que
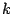 es factor de
es factor de 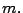 Por lo tanto
Por lo tanto
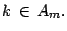
- Sea
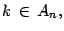 entonces existe
entonces existe
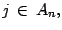 tal que
tal que 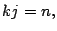 por lo tanto
por lo tanto
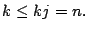
- De la justificación del resultado
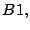 se tiene que
se tiene que
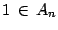 y
y
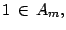 para cualesquiera
naturales
para cualesquiera
naturales  y
y
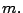
El conjunto
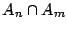 es llamado el conjunto de los divisores
comunes de
es llamado el conjunto de los divisores
comunes de  y
y 
Definición 3.
Se define el máximo común divisor de los
números naturales  y
y  como el máximo del conjunto
formado por los divisores comunes de
como el máximo del conjunto
formado por los divisores comunes de  y
y  . Se denota por
. Se denota por
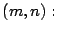
El máximo común divisor esta bien definido debido que
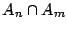 es diferente de vacío (resultado
es diferente de vacío (resultado 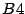 ) y es acotado, pues
) y es acotado, pues 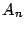 y
y 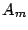 son acotados (resultado
son acotados (resultado 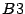 ), por lo tanto
), por lo tanto
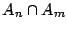 es un
conjunto infinito no vacío.
es un
conjunto infinito no vacío.
- Ejemplo 4.
-
- Determine
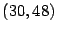
- Solución.
-
- Note que
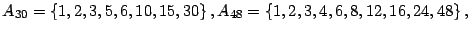 entonces
entonces
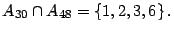 Por lo tanto
Por lo tanto
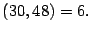
Más adelante veremos un algoritmo que permite hallar el máximo
común divisor de una manera más rápida.
Definición 4.
Se define el conjunto 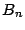 como el conjunto formado por todos los
múltiplos de
como el conjunto formado por todos los
múltiplos de 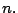
Ejemplo 5.
El con junto 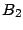 es el conjunto de los números
pares. Por otro lado,
es el conjunto de los números
pares. Por otro lado,
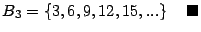
Algunas de las propiedades del conjunto  se muestran a
continuación.
se muestran a
continuación.
- Grupo de Resultados C.
- Para todo
 es diferente del vacío
es diferente del vacío
- Si
 es divisor de
es divisor de  entonces
entonces
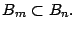
- El mínimo valor de
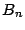 es
es 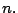
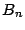 no posee un elemento máximo.
no posee un elemento máximo.
- Para cualesquiera números naturales
 y
y 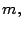 se tiene que
se tiene que
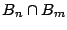 es diferente del conjunto
es diferente del conjunto
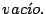
- Justificación de los resultados C.
- Como
 es múltiplo de
es múltiplo de  entonces
entonces
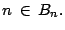
- Sea
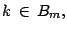 entonces
entonces  es divisor de
es divisor de 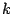 y
como
y
como  es divisor de
es divisor de 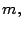 por el resultado
por el resultado 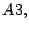 se concluye que
se concluye que
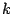 es múltiplo de
es múltiplo de 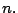
- Si
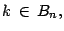 entonces existe un número
natural
entonces existe un número
natural 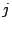 tal que
tal que 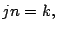 por lo tanto,
por lo tanto,
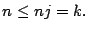
- Si
 es el máximo de
es el máximo de 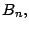 entonces
entonces
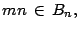 pues
pues 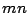 es un múltiplo de
es un múltiplo de 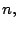 así se llega a
una contradicción.
así se llega a
una contradicción.
- Note que
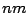 es múltiplo de
es múltiplo de  y de
y de 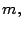 por lo tanto
por lo tanto
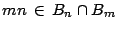
El conjunto
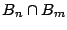 suele ser llamado como el conjunto de
los múltiplos comunes de
suele ser llamado como el conjunto de
los múltiplos comunes de  y
y
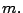
Definición 5.
Se define el mínimo común múltiplo de los números
naturales  y
y  como el mínimo valor del conjunto formado por los
múltiplos comunes de
como el mínimo valor del conjunto formado por los
múltiplos comunes de  y
y 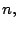 se denota por
se denota por
![$ \left[ m,n\right] .$](img99.gif) Es
decir
Es
decir
Al igual que el máximo común divisor, el mínimo común
múltiplo esta definido debido que
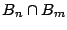 es diferente de
vacío (resultado
es diferente de
vacío (resultado 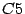 )
y además )
y además
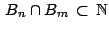
- Ejemplo 6.
-
- Determine el mínimo común múltiplo de
![$ \left[
30,48\right] $](img103.gif)
- Solución.
-
- Se tiene que
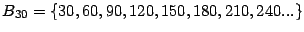 y
y
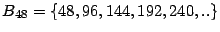 por lo tanto
por lo tanto
![$ \left[ 30,48\right]
=\min\left( B_{30}\cap B_{48}\right) =240. %
\medskip\medskip$](img106.gif)
Note que calcular un mínimo común múltiplo utilizando la
definición no es un algoritmo muy eficiente, más adelante se brinda
una manera más eficiente de calcularlo.
Definición 6
Se dice que un número natural 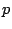 es primo si tiene solamente dos
divisores, es decir
es primo si tiene solamente dos
divisores, es decir
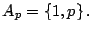 Si un número tiene
más de dos divisores se dice que es compuesto.
Si un número tiene
más de dos divisores se dice que es compuesto.
- Ejemplo 7.
-
- Los números:
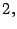
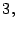
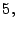
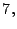
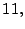
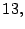
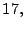
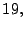
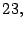
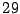 son los primeros diez primos.
son los primeros diez primos.

Uno de los resultados más importantes en Teoría de Números es el
Teorema Fundamental de la Aritmética: Todo número natural
puede expresarse como una multiplicación de números
primos''. Más aun, si dichos factores se ordenan de manera
ascendente, la forma de expresar el número
Todo número natural
puede expresarse como una multiplicación de números
primos''. Más aun, si dichos factores se ordenan de manera
ascendente, la forma de expresar el número  es única, o sea
es única, o sea  puede escribirse de manera única así:
puede escribirse de manera única así:
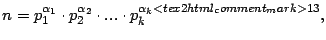 donde donde 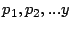 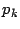 son primos y además son primos y además 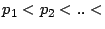 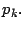 |
(1) |
La demostración de este teorema se puede consultar en casi cualquier libro
de Teoría de Números.
- Ejemplo 8.
-
-
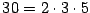
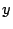
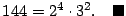
Se entenderá por factorización prima de  , la expresión de
, la expresión de  de la forma dada en
de la forma dada en
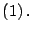 Como consecuencia de
este teorema, se obtiene un resultado que simplifica el cálculo del
máximo común divisor y el mínimo común múltiplo:
Como consecuencia de
este teorema, se obtiene un resultado que simplifica el cálculo del
máximo común divisor y el mínimo común múltiplo:
Teorema. Sea
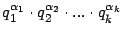 y
y
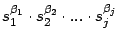 la factorización prima de
la factorización prima de  y
y  respectivamente.
respectivamente.
- a)
- Tomemos todos los primos involucrados en la factorización prima
de
 y
y
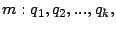
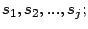 y
reordenémonos de menor a mayor, entonces,
y
reordenémonos de menor a mayor, entonces,  y
y  se pueden escribir de
la siguiente manera:
se pueden escribir de
la siguiente manera:
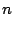 |
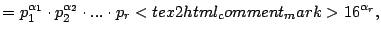 donde si donde si 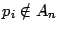 se define se define 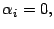 |
|
 |
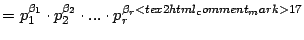 donde si donde si 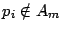 se define se define 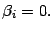 |
|
- b)
- Utilizando la notación de
 y
y  dada por la parte
dada por la parte  se
tiene que:
se
tiene que:
-
- Ejemplo
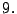
-
- Determine
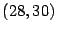 y
y
![$ \left[
28,30\right] $](img148.gif)
- Solución.
-
- La factorización de 28 y 30 es respectivamente
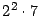 y
y
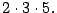 Así, estos números se puede escribir
como
Así, estos números se puede escribir
como
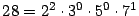 y
y
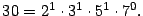 Por lo tanto
Por lo tanto
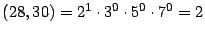 y
y
![$ \left[ 28,30\right]
=2^{2}\cdot3^{1}\cdot 5^{1}\cdot7^{1}=420. \medskip\medskip$](img154.gif)
En la practica, el lector puede apreciar que se puede omitir la notación
dada en el teorema anterior. A raíz del Teorema Fundamental de la
Aritmética surgen varios métodos para hallar la factorización
prima de un número natural, que se estudiarán en la siguiente
sección, los cuales permitirán de acuerdo al teorema anterior, hallar
de una manera más ágil el máximo común divisor y el
mínimo común múltiplo.
Revista digital Matemática, Educación e Internet.
Derechos Reservados
|