|
Los métodos de factorización prima son algoritmos que
permiten hallar los factores primos de un número. Dichos
algoritmos se puede clasificar en: factorización por factores
primos y por factores compuestos. Para el desarrollo de estos
algoritmos es indispensable identificar los números primos,
por ello, al final del presente trabajo se brinda una tabla con
los números primos menores que 200. Seguidamente se explican
cada una de estos tipos de métodos de factorización
prima.
Métodos de factorización por factores primos.
Estos métodos son la aplicación directa del teorema de
factorización prima, pues da un número natural  consisten en hallar
de manera ascendente cada uno de los factores primos de
consisten en hallar
de manera ascendente cada uno de los factores primos de 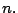 En forma general
estos algoritmos siguen los siguientes pasos:
En forma general
estos algoritmos siguen los siguientes pasos:
- Paso 1.
-
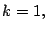
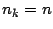
- Paso 2.
-
- Determinar el número primo más pequeño que divide a
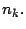 Este sera llamado
Este sera llamado 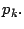
- Paso 3.
-
- Se define
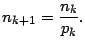
- Paso 4.
-
- Si
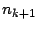 es primo entonces finaliza el procedimiento y se
obtiene que
es primo entonces finaliza el procedimiento y se
obtiene que
donde
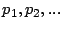
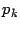 y
y 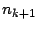 son primos y además
son primos y además
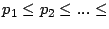
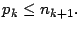 Si no se pasa al paso 5
Si no se pasa al paso 5
- Paso 5.
-
- Incrementar
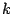 en una unidad y pasar al paso 2.
en una unidad y pasar al paso 2.
Básicamente, estos métodos siguen un procedimiento de
búsquedad lineal, es decir no se puede determinar el
k-ésimo primo, 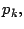 si no se han determinado todos los
anteriores:
si no se han determinado todos los
anteriores:
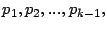 lo que provoca que estos
métodos sea muy ineficientes para números grandes. A
continuación se presentan los dos métodos que obedecen
este procedimiento.
lo que provoca que estos
métodos sea muy ineficientes para números grandes. A
continuación se presentan los dos métodos que obedecen
este procedimiento.
Método de ensayo y error.
En este método, para el paso 2 se procede realizando la división de
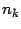 entre
entre
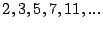 hasta obtener el primer primo divisor de
hasta obtener el primer primo divisor de
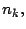 veamos el siguiente ejemplo.
veamos el siguiente ejemplo.
- Ejemplo 1.
-
- Determine la factorización prima de
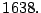
- Solución.
-
- Los resultados del método ensayo y error se presentan
en la siguiente tabla
Así, en este caso se obtiene que
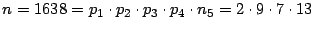
-
Método por reglas de divisibilidad.
Este método es una variación del anterior y consiste en sustituir
algunas de las divisiones por reglas de divisibilidad. Para efectos de dicha
presentación se enumeran seguidamente.
Dado un número 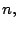 se dice que
se dice que
 es divisible entre
es divisible entre 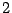 si su último digito es
si su último digito es 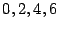
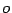
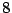
 es divisible entre
es divisible entre 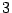 si la suma de sus dígitos es
múltiplo de
si la suma de sus dígitos es
múltiplo de 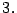
 es divisible entre
es divisible entre 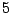 si su último digito es 0
si su último digito es 0
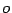
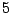
 es divisible entre
es divisible entre 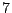 si el número que queda suprimiendo el
dígito de de las unidades, disminuido en el doble de las unidades es 0
o múltiplo de
si el número que queda suprimiendo el
dígito de de las unidades, disminuido en el doble de las unidades es 0
o múltiplo de 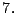
 es divisible entre
es divisible entre 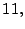 si la suma de los dígitos de las
posiciones pares menos la suma de los dígitos de las posiciones impares
es 0
o múltiplo de
si la suma de los dígitos de las
posiciones pares menos la suma de los dígitos de las posiciones impares
es 0
o múltiplo de 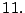
-
- Ejemplo 2.
-
- Determine la factorización prima de
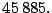
- Solución.
-
- Los resultados del método por reglas de divisibilidad
se observan en la siguiente tabla.
Por lo tanto se realiza
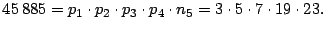
-
Nota: Esta tabla como la del ejemplo anterior, es una manera
de exhibir los resultados del método posterior a su
aplicación, pues una vez aplicado el método, se sabe
cuantas columnas se requieren.
Si bien este método es más eficiente que el anterior, se puede
mejorar. En efecto, la idea consiste en romper el orden de menor a mayor de
los primos y verificar primero si el 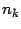 es divisible por 5 y luego por 2,
que es fácil de comprobarlo. Esto permitirá obtener luego un
es divisible por 5 y luego por 2,
que es fácil de comprobarlo. Esto permitirá obtener luego un 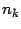 más cómodo para determinar si es divisible por
más cómodo para determinar si es divisible por
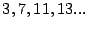
Hasta el momento se han presentado en los ejemplos, unas tablas que ilustran
muy bien el procedimiento de los algoritmos utilizados. Sin embargo, en
secundaria se utiliza una tabla donde se suele omitir el paso 2 de los
algoritmos, las cuales tienen la ventaja de que se puede utilizar para ir
presentado los datos conforme el método avanza, y no como en las
anteriores, en donde no se podía construir la tabla hasta que el
algoritmo finalice. El docente puede optar en un primer momento, por utilizar
tablas similares a las expuestas en los ejemplos, permitiendo que los alumnos
se familiaricen con los algoritmos, y posteriormente, utilizar la tradicional
tabla que se expone en el siguiente ejemplo.
- Ejemplo 3.
-
- Determine la factorización prima de
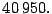
- Solución.
-
- Aplicando el algoritmo se tiene que
Por lo tanto
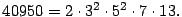
Desventajas de los métodos por factores primos.
Como se han mencionado anteriormente, una de las mayores desventajas de estos
métodos de factorización de un número natural  es que utilizan
un procedimiento de búsquedad lineal para hallar los factores primos de
es que utilizan
un procedimiento de búsquedad lineal para hallar los factores primos de
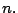 Otras desventajas que tienen estos métodos son:
Otras desventajas que tienen estos métodos son:
- Funcionan sólo para números "pequeños". Para números muy
grandes estos algoritmos requieren mucho tiempo.
- Se cuenta con pocas reglas de divisibilidad. Estás son sólo para
los primeros primos.
- Es complicado saber si un número mayor que 100 es primo. La
mayoría de personas conocen a lo sumo los veinte primeros números.
Esto provoca que si
 esta compuesto con primos mayores que 100, se une al
algoritmo la dificultad de tener que ir determinando los primos en el orden
que se sigue.
esta compuesto con primos mayores que 100, se une al
algoritmo la dificultad de tener que ir determinando los primos en el orden
que se sigue.
Métodos de factorización por factores compuestos.
Estos métodos consisten en, dado un número natural 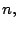 hallar dos
números
hallar dos
números  y
y 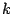 (no necesariamente primos) que cumplan
(no necesariamente primos) que cumplan 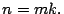 De manera
general, estos algoritmos siguen los siguientes pasos para la
factorización de
De manera
general, estos algoritmos siguen los siguientes pasos para la
factorización de  :
:
- Paso 1.
-
- Hallar dos números naturales
 y
y 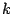 que cumplan que
que cumplan que
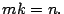
- Paso 2.
-
- Factorizar
 y
y 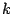 utilizando algunos de los métodos de
factorización.
utilizando algunos de los métodos de
factorización.
-
Si se continúa aplicando este mismo tipo de método, se
puede apreciar que se sigue un procedimiento de búsqueda de
árbol, pues se va simultáneamente hallando los factores
primos de 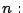
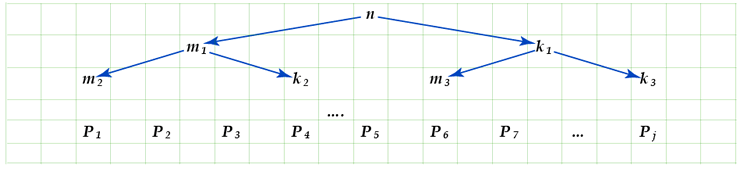
Veamos el siguiente ejemplo.
- Ejemplo 4.
-
- Determine la factorización prima de
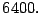
- Solución.
-
- Se tiene que
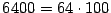 y como
y como
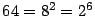 y
y
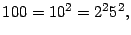 entonces
entonces
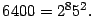
No siempre es tan fácil determinar para un número natural
 dos números que multiplicados entre sí den como
resultado
dos números que multiplicados entre sí den como
resultado 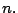 Es fácil cuando el número es divisible por
Es fácil cuando el número es divisible por
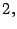
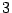 o
o 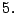 Por lo tanto, en los métodos que presentaremos
en las secciones siguientes se asumirá que el número
Por lo tanto, en los métodos que presentaremos
en las secciones siguientes se asumirá que el número  a
factorizar es impar y no es divisible por 3 ni por 5, pues, en
caso contrario, es mejor aplicar inicialmente algunos de los
métodos vistos, hasta obtener factores (un valor
a
factorizar es impar y no es divisible por 3 ni por 5, pues, en
caso contrario, es mejor aplicar inicialmente algunos de los
métodos vistos, hasta obtener factores (un valor 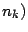 que
cumplan dicho supuesto.
que
cumplan dicho supuesto.
Método de factorización de Fermat
Sea  un número natural impar, se quiere hallar dos naturales
un número natural impar, se quiere hallar dos naturales  y
y 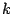 que cumplan
que cumplan
Como  es impar entonces tanto
es impar entonces tanto  como
como 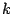 son impares y suponiendo sin
pérdida de generalidad que
son impares y suponiendo sin
pérdida de generalidad que 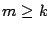 entonces,
entonces,
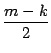 y
y
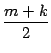 son números naturales. Tómese
son números naturales. Tómese
Note que
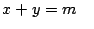 y
y
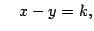 por lo tanto
por lo tanto
Así, nuestro problema se reduce ha hallar dos números naturales 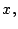
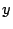 que cumplan
que cumplan
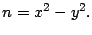
Note que de
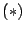 se tiene que
se tiene que
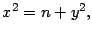 entonces
entonces
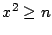 y se sigue que
y se sigue que
Por otro lado, de
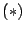 se deduce que
se deduce que 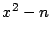 debe ser un
cuadrado perfecto, que se denotará por
debe ser un
cuadrado perfecto, que se denotará por
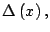 por lo
tanto
por lo
tanto
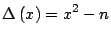 debe ser un cuadrado perfecto 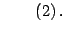
En resumen a partir de
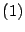 y
y
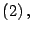 el
Método de Fermat sigue los siguientes pasos, para determinar los factores
el
Método de Fermat sigue los siguientes pasos, para determinar los factores
 y
y 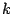 de un número natural
de un número natural  :
:
- Paso 1.
-
- Si
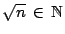 tome
tome
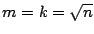 y
finaliza el algoritmo. Sino pase al paso
y
finaliza el algoritmo. Sino pase al paso 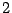
- Paso 2.
-
- Sea k el número natural entre
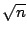 y
y
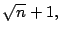 pase al paso siguiente
pase al paso siguiente
- Paso 3.
-
- Si
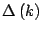 es cuadrado perfecto tome
es cuadrado perfecto tome 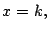
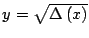 ,
, 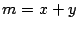 ,
, 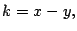 y finaliza el
algoritmo. Si no, pase al paso siguiente.
y finaliza el
algoritmo. Si no, pase al paso siguiente.
- Paso 4.
-
- Incremente
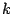 en una unidad y pase al paso anterior.
en una unidad y pase al paso anterior.
- Ejemplo 5.
-
- Determine la factorización prima de
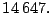
- Solución.
-
- En este caso se tiene que
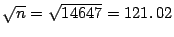 por lo tanto se debe buscar un número
por lo tanto se debe buscar un número
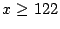 que cumpla:
que cumpla:
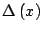 se un cuadrado perfecto. Por
lo tanto se procede de manera inductiva sobre
se un cuadrado perfecto. Por
lo tanto se procede de manera inductiva sobre 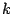 a partir de
a partir de 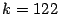 hasta
obtener que
hasta
obtener que
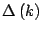 sea un cuadrado perfecto:
sea un cuadrado perfecto:
Por lo tanto 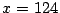 ,
, 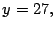 y se obtiene que el número
y se obtiene que el número 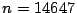 puede
ser factorizado por
puede
ser factorizado por
Como 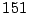 y
y 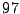 son primos, entonces dicha factorización es
la factorización prima de
son primos, entonces dicha factorización es
la factorización prima de
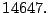
Ahora bien, este método se puede mejorar si se halla una fórmula
recursiva para
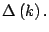 En efecto, note que
En efecto, note que
Dicha fórmula facilita el cálculo de
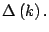
El siguiente ejemplo muestra que a pesar de que el Método de Fermat
requiere menos tiempo que los anteriores, no es tan rápido.

- Ejemplo 6.
-
- Determine la factorización prima de
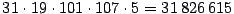
- Solución.
- Note que este número es divisible entre
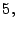 por lo
tanto nos interesa factorizar
por lo
tanto nos interesa factorizar
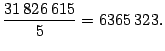 Sea
Sea
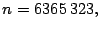 se tiene que
se tiene que
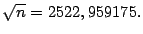 Por lo tanto, se obtiene
que
Por lo tanto, se obtiene
que
![$\displaystyle \begin{tabular}[c]{\vert c\vert c\vert c\vert}\hline \multicolumn...
...8$\ & $544,2775028$\\ \hline
$2582$\ & $301401$\ & $549$\\ \hline
\end{tabular}$](img254.gif)
Así,
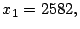
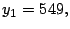
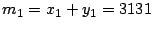 y
y
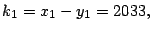 por lo tanto
por lo tanto
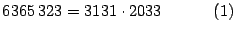
Ahora, factoricemos 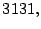 note que
note que
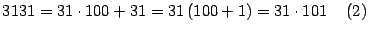
Por otro lado, utilicemos el método de Fermat para factorizar 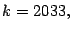 donde
donde
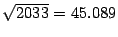 . Se sigue que
. Se sigue que
![$\displaystyle \begin{tabular}[c]{\vert c\vert c\vert c\vert}\hline \multicolumn...
... $1811$\ & $42,55584566$\\ \hline
$63$\ & $1936$\ & $44$\\ \hline
\end{tabular}$](img264.gif)
Así, se obtiene que
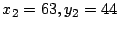 ,
,
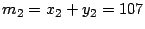 y
y
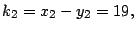 entonces
entonces
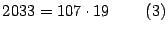
Por
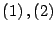 y
y
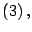 se
concluye que
se
concluye que
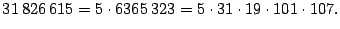
Método de Factorización de Euler
Suponga que el número impar  a factorizar puede ser representado en dos
formas distintas, como la suma de dos cuadrados perfectos:
a factorizar puede ser representado en dos
formas distintas, como la suma de dos cuadrados perfectos:
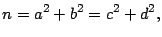 con 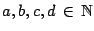
Como 
es impar, entonces solo puede ser expresado como la suma de un impar
y un par, por lo tanto, supongamos sin perdida de generalidad que 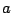
y 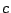
son números impares, en tanto, 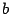
y 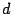
son pares, y además 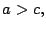
por lo tanto 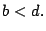
Debido a esto, note que 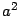
es de la forma 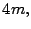
mientras 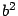
es de la forma 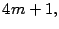
por lo tanto, 
es de la forma
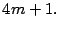
Por otro lado, de
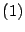 se tiene que
se tiene que
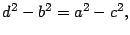 y se sigue que
y se sigue que
Sea
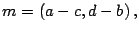 por lo tanto existen dos números
naturales
por lo tanto existen dos números
naturales 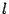 y
y 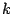 que cumplen:
que cumplen:
Note que 
es par, pues 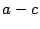
y 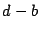
son pares. Sustituyendo
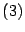
en
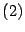
se obtiene que
Como
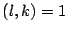
entonces 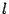
es divisor de
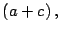
y entonces existe un número natural 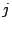
que cumple
Sustituyendo
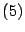
en
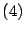
se sigue
Debido a
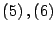
y
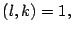
se obtiene que
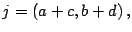
y como 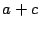
y 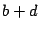
son pares se
concluye que 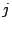
es par.
Dado que  y
y 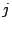 son números pares, verifiquemos que una
factorización de
son números pares, verifiquemos que una
factorización de  está dada por
está dada por
En efecto, expandiendo
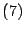
se obtiene que
aplicando
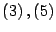
y
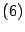
se
deduce que
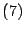
es equivalente a
Lo anterior justifica el Método de Euler que se enuncia en las siguientes
líneas.
En resumen, para poder factorizar un número impar  con el Método de
Euler, este debe cumplir:
con el Método de
Euler, este debe cumplir:
- Es de la forma
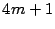 .
.
- Se puede representar como la suma de dos cuadrados perfectos:
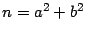 , con
, con 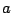 impar y
impar y 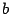 par.
par.
- Posee otra representación como la suma de dos cuadrados perfectos:
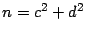 , con
, con 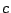 impar y
impar y 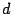 par.
par.
Así para un  que cumple con las reglas anteriores, se puede factorizar
siguiendo los siguientes pasos:
que cumple con las reglas anteriores, se puede factorizar
siguiendo los siguientes pasos:
- Paso 1.
-
- Calcular
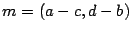
- Paso 2.
-
- Hallar
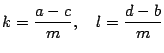
- Paso 3.
-
- Determinar
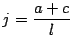
- Paso 4.
- La factorización de
 esta dada por
esta dada por
![$ \left[ \left(
\dfrac{m}{2}\right) ^{2}+\left( \dfrac{j}{2}\right) ^{2}\right] \left[
\left( l\right) ^{2}+\left( k\right) ^{2}\right] \medskip\medskip .$](img321.gif)
- Ejemplo 7.
-
- Determine la factorización prima de
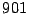
- Solución.
-
- Dado que
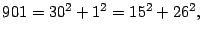 se tiene que
se tiene que
Por lo tanto,
El principal inconveniente de este método es la determinación de 2
representaciones del número  a factorizar como la suma de dos
cuadrados. Sin embargo, al igual que en el Método de Fermat, se puede
buscar por medio de una tabla, dos valores enteros de
a factorizar como la suma de dos
cuadrados. Sin embargo, al igual que en el Método de Fermat, se puede
buscar por medio de una tabla, dos valores enteros de 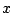 entre
entre 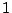 y
y
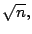 para los cuales
para los cuales
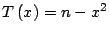 es un cuadrado
perfecto
es un cuadrado
perfecto En caso de que existan dichos valores de
En caso de que existan dichos valores de 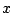 , digamos
, digamos 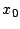 y
y
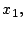 se obtiene que
se obtiene que  tiene 2 representaciones como la suma de dos
cuadrados:
tiene 2 representaciones como la suma de dos
cuadrados:
Además, se puede establecer una fórmula recursiva para
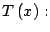
- Ejemplo 8.
-
- Determine la factorización prima de
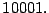
- Solución.
-
- En la siguiente tabla se aprecian los valores de
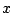 y
y
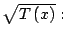
Así, se tiene que
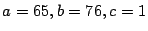 y
y 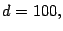 además
además
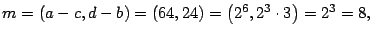 con estos valores se obtiene:
con estos valores se obtiene:
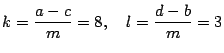 y
y
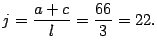 Por lo tanto, la
factorización prima de 10001 es
Por lo tanto, la
factorización prima de 10001 es
- Ejemplo 9.
-
- Determine la factorización prima de
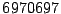
- Solución.
-
- Note que
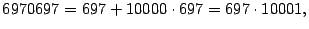 y por
el ejercicio anterior se sabe que la factorización prima de
y por
el ejercicio anterior se sabe que la factorización prima de
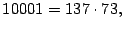 por lo que solo resta factorizar
por lo que solo resta factorizar 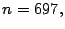 para el cual se
tiene los siguientes valores de
para el cual se
tiene los siguientes valores de 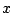 y
y
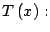
Así, se obtiene que
Por lo tanto
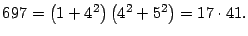 Se concluye que la factorización prima de
Se concluye que la factorización prima de 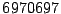 es
es
Con este ejemplo se finaliza esta presentación, esperamos que esta sea de
utilidad al lector.
Revista digital Matemática, Educación e Internet.
Derechos Reservados
|
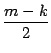 y
y
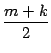 son números naturales. Tómese
son números naturales. Tómese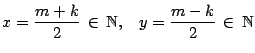
![\begin{displaymath}
\begin{tabular}[c]{\vert c\vert c\vert ccccc}\hline \multico...
...}[c]{ll}
& \\
&
\end{tabular}& & \\ \cline{1-2}%
\end{tabular}\end{displaymath}](img180.gif)
![$\displaystyle \begin{tabular}[c]{\vert c\vert c\vert ccccccccc}\hline \multicol...
...\begin{tabular}[c]{ll}
& \\
&
\end{tabular}& & & \\ \cline{1-2}%
\end{tabular}$](img192.gif)
![$\displaystyle \begin{tabular}[c]{c\vert c}%
$n_{k}$\ & $p_{k}$\\ \hline
$40950$...
...rac{91}{7}=$\ $13$\ &
\begin{tabular}[c]{ll}
& \\
&
\end{tabular}\end{tabular}$](img196.gif)

![$\displaystyle \begin{tabular}[c]{\vert c\vert c\vert c\vert}\hline \multicolumn...
... & $482$\ & $21,9544984$\\ \hline
$124$\ & $729$\ & $27$\\ \hline
\end{tabular}$](img240.gif)
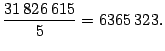 Sea
Sea
![$\displaystyle \begin{tabular}[c]{\vert c\vert c\vert c\vert}\hline \multicolumn...
...8$\ & $544,2775028$\\ \hline
$2582$\ & $301401$\ & $549$\\ \hline
\end{tabular}$](img254.gif)
![$\displaystyle \begin{tabular}[c]{\vert c\vert c\vert c\vert}\hline \multicolumn...
... $1811$\ & $42,55584566$\\ \hline
$63$\ & $1936$\ & $44$\\ \hline
\end{tabular}$](img264.gif)
![$\displaystyle \left[ \left( \dfrac{m}{2}\right) ^{2}+\left( \dfrac{j}{2}\right)...
...ft[ \left( l\right) ^{2}+\left( k\right) ^{2}\right]
\quad\quad\left( 7\right)
$](img309.gif)
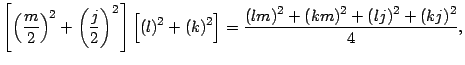
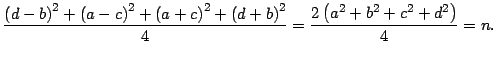
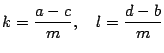
![$ \left[ \left(
\dfrac{m}{2}\right) ^{2}+\left( \dfrac{j}{2}\right) ^{2}\right] \left[
\left( l\right) ^{2}+\left( k\right) ^{2}\right] \medskip\medskip .$](img321.gif)
![$\displaystyle \begin{tabular}[c]{lllll}%
$a=$\ & $15$\ & & $m=$\ & $\left( 14,4...
...\
$c=$\ & $1$\ & & $l=$\ & $2$\\
$d=$\ & $30$\ & & $j=$\ & $8$%
\end{tabular}$](img324.gif)
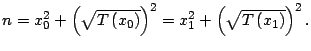
![$\displaystyle \begin{tabular}[c]{\vert c\vert c\vert c\vert}\hline \multicolumn...
...\ & $\vdots$\ & $\vdots$\\ \hline
$76$\ & $4225$\ & $65$\\ \hline
\end{tabular}$](img336.gif)
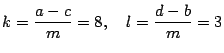 y
y
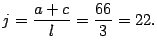 Por lo tanto, la
factorización prima de 10001 es
Por lo tanto, la
factorización prima de 10001 es
![$\displaystyle 10001=\left[ \left( \dfrac{m}{2}\right) ^{2}+\left(
\dfrac{j}{2}\...
...{2}\right] =\left( 4^{2}+11^{2}\right)
\left( 3^{2}+8^{2}\right) =137\cdot 73.
$](img342.gif)
![$\displaystyle \begin{tabular}[c]{\vert c\vert c\vert c\vert}\hline \multicolumn...
...$\ & $\vdots$\ &
$\vdots$\\ \hline $16$\ & $441$\ & $21$\\ \hline
\end{tabular}$](img347.gif)
![$\displaystyle \begin{tabular}[c]{lllll}%
$a=$\ & $21$\ & & $m=$\ & $\left( 10,8...
...
$c=$\ & $11$\ & & $l=$\ & $4$\\
$d=$\ & $24$\ & & $j=$\ & $8$%
\end{tabular}$](img348.gif)