¿Cómo demostrar que
|
es
verdadero?
 |
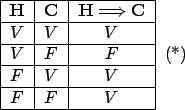Si se quiere que
sea verdadero, basta
probar que el caso
no se cumple. Es decir, es
suficiente demostrar si 
es verdadero entonces se puede deducir que 
es verdadero y por lo tanto no se puede dar el caso en que
sea falso. De lo anterior, parece razonable
denominar a 
hipótesis (proposición cuyo valor de verdad
se asume) y a 
conclusión (proposición cuyo valor de
verdad se desea averiguar. Si por el contrario a partir de 
y de otras
proposiciones verdaderas de la teoría se deduce
entonces
es una contingencia y no una falacia.
En uno proceso de demostración de
se utiliza además de 
otras hipótesis que
no son mencionadas, estas pueden ser axiomas o teoremas.
De esta manera, se concluye que para demostrar una implicación, debe asumirse la veracidad de la hipótesis y se deduce que la conclusión es verdadera. Esta conclusión se debe evidenciar en la demostración de implicaciones:
 |
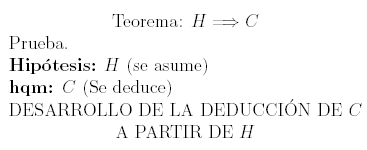La manera en que se realice la deducción de 
a partir de 
obedece
a un método de demostración, por el cuál entenderemos un modelo
a seguir para resolver el problema de la demostración. Desde este
enfoque no se considera a la contrapositiva como un método de demostración de implicaciones, sino como una herramienta que me permite
transformar el problema. El uso de la contrapositiva en la demostración
sigue el siguiente modelo:
 |
Como se observa la contrapositiva transforma la implicación en otra
implicación, donde la deducción de la conclusión a partir de la
hipótesis se debe de realizar utilizando alguno de los métodos de
demostración. Seguidamente se expondrán los métodos de demostración de implicaciones más comunes.
| Inicio 1 2 3 4 5 6 7 |
|
Cidse
- Revista
virtual Matemática, Educación e Internet -
ITCR
Derechos Reservados