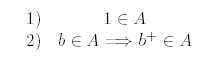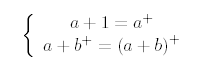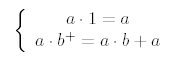|
- Sea
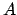 un conjunto de números reales que cumple las siguientes
proposiciones (axiomas): un conjunto de números reales que cumple las siguientes
proposiciones (axiomas):
Demuestre los siguientes teoremas utilizando el método indicado.
-
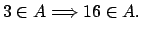
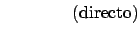
-
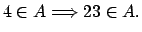
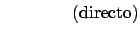
-
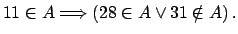
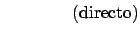
-
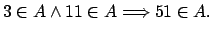
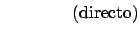
-
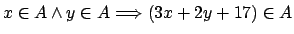
-
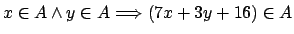
-
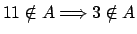

-
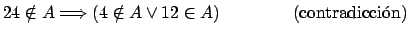
-
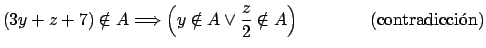
-
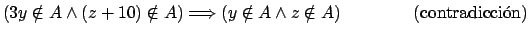
-
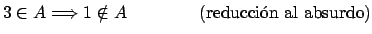
-

-
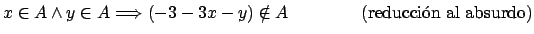
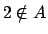
-
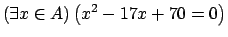
- Sea
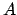 un conjunto de números reales que cumple (axioma): un conjunto de números reales que cumple (axioma):
Determine si las siguientes proposiciones son verdaderas o falsas. Si son
verdaderas demuéstrelas y si no, brinde un contraejemplo (indique un
conjunto 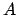 que cumple las hipótesis pero no la conclusión). Nota: que cumple las hipótesis pero no la conclusión). Nota:
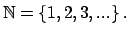
-
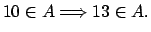
-
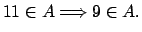
-
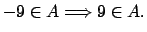
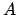 puede ser el conjunto puede ser el conjunto
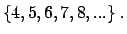
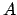 puede ser el conjunto puede ser el conjunto
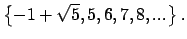
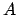 puede ser el conjunto puede ser el conjunto
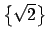
-
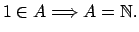
-
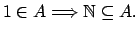
-
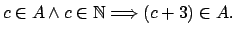
-
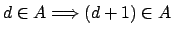
-
![$ m\in A\Longrightarrow \left( \forall p\in
\mathbb{N}
\right) \left[ \left( n+p\right) \in A\right] $](img214.gif)
-
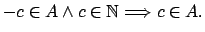
-
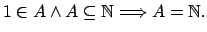
- Construcción del conjunto de los números naturales.
 La idea es construir formalmente este conjunto(suponga que no lo conoce) a
partir de La idea es construir formalmente este conjunto(suponga que no lo conoce) a
partir de 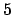 axiomas (Los Axiomas de Peano): axiomas (Los Axiomas de Peano):
- Axioma 1.
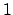 es un numero natural. es un numero natural.
- Axioma 2.
- Para todo
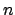 numero natural, existe un único número natural numero natural, existe un único número natural 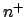 llamado el sucesor de llamado el sucesor de 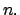
- Axioma 3.
- El número natural
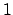 no es sucesor de algún número natural. no es sucesor de algún número natural.
- Axioma 4.
- Si
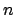 y y 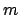 son números naturales tales que son números naturales tales que
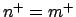 (el sucesor de (el sucesor de 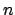 es igual al sucesor de es igual al sucesor de 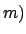 entonces entonces 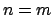
- Axioma 5.
- Si
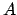 es un conjunto formado por números naturales
que cumple: es un conjunto formado por números naturales
que cumple:
entonces 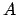 es el conjunto de los números naturales, denotado por es el conjunto de los números naturales, denotado por
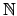 . .
 Se denota Se denota 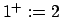 y y
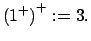 Utilice estos axiomas
para demostrar los siguientes teoremas. Utilice estos axiomas
para demostrar los siguientes teoremas.
- Pruebe que no existe un número natural
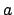 tal que tal que
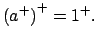
- Pruebe que
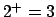
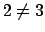
- Si
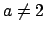 entonces entonces
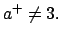
- Si
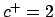 entonces entonces 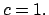
- Pruebe que el conjunto
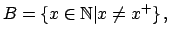 cumple las condiciones del axioma cumple las condiciones del axioma 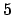 y por lo tanto y por lo tanto
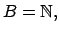 es decir, ningún número natural es igual a su sucesor. es decir, ningún número natural es igual a su sucesor.
- Se define la suma de números naturales como la operación
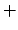 que cumple:
que cumple:
Pruebe que
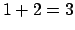
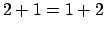
-
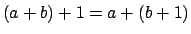
- Se define el producto de números naturales como la operación
 que cumple: que cumple:
Pruebe que
-
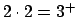
-
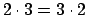
-
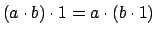
-
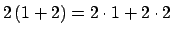
Este documento fue generado usando
LaTeX2HTML translator Version 2002-2-1 (1.71)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
Cidse
- Revista
virtual Matemática, Educación e Internet -
ITCR
Derechos Reservados
|