|
En este método se parte de que 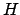 es verdadero y por medio de las reglas de inferencias, leyes de la
lógica, axiomas, definiciones o teoremas, se deduce que es verdadero y por medio de las reglas de inferencias, leyes de la
lógica, axiomas, definiciones o teoremas, se deduce que 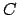 es verdadero. Un modelo para este método es: es verdadero. Un modelo para este método es:
Observaciones:
- Note que en realidad a partir de los teoremas definiciones o axiomas, entre
otros, se tienen las siguientes implicaciones tautológicas:
Al asumir que 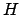 es verdadero, aplicando las reglas de inferencia (Modus Ponens y
adjunción) se tiene que es verdadero, aplicando las reglas de inferencia (Modus Ponens y
adjunción) se tiene que 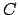 es verdadero. En efecto, si es verdadero. En efecto, si
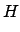 es verdadero, es verdadero,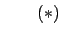 |
|
por Modus Ponens a
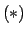 y y
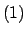 se tiene que se tiene que
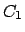 es verdadero. es verdadero. |
|
Por adjunción, se tiene que
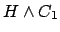 es verdadero, es verdadero,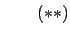 |
|
y nuevamente por Modus Ponens a
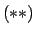 y y
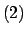 se tiene que se tiene que
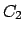 es verdadero. es verdadero. |
|
El proceso de deducción continúa hasta llegar a que 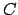 es verdadero. es verdadero. 
- En el modelo, cada deducción es conveniente justificarla, indicando las
premisas, reglas, axiomas o teoremas en que se basó.
Ejemplo 1 Sea 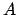 un conjunto de números reales que cumple las siguientes
proposiciones (axiomas):
Pruebe las siguientes proposiciones.  Teorema Teorema 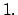 Si 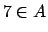 entonces
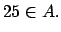 Teorema Teorema 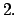 Si 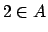 entonces
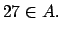
- Prueba.
- Utilizaremos el método directo para demostrarlos.
|