|
Este método suele ser confundido con el método de contradicción. Cuando se
realiza una prueba utilizando reducción al absurdo se suele seguir el siguiente
modelo
La gran diferencia con el método de contradicción es que en este método se
utiliza la hipótesis y la negación de la contradicción para llegar a un absurdo.

Ejemplo 3 Sea 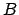 un conjunto de números reales que cumple las siguientes
proposiciones (axiomas):
Pruebe las siguientes proposiciones. 
Teorema 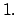 Se cumple que: Se cumple que:
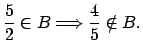
Teorema 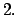 Si Si
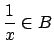 entonces entonces
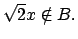
- Prueba.
- Utilizaremos el método de reducción al absurdo para demostrarlos.
Finalmente, observemos un ejemplo de un estructura donde se combinan los métodos
vistos para demostrar los teoremas.
Ejemplo 4 Considere las siguientes proposiciones:
- Definición 1.
-
- Una palabra es invertible, si es permitida y la palabra que se obtiene al
invertir el orden de sus letras es permitida

- Definición 2.
-
- Se dice que
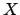 es una palabra permitida, o simplemente que es permitida, si es una palabra permitida, o simplemente que es permitida, si 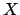 es una sucesión de letras tomadas de es una sucesión de letras tomadas de
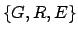 que es permitida. que es permitida.
- Axioma 1.
-
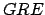 es permitida es permitida
- Axioma 2.
- Si una palabra con dos
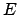 seguidas es permitida entonces la palabra que se obtiene al
eliminar las dos seguidas es permitida entonces la palabra que se obtiene al
eliminar las dos 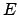 seguidas es permitida. seguidas es permitida.
- Axioma 3.
- Una palabra con una
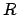 es permitida si y solo si la palabra que se obtiene al cambiar la es permitida si y solo si la palabra que se obtiene al cambiar la 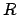 por por 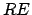 es permitida. es permitida.
- Axioma 4.
- Si
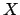 y y 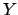 son permitidas entonces la palabra son permitidas entonces la palabra 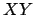 es permitida. es permitida.
- Axioma 5.
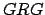 no es permitida. no es permitida.
 Pruebe los siguientes proposiciones. Pruebe los siguientes proposiciones.
- Teorema
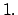
- Se tiene que
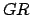 es permitida. es permitida.
- Teorema
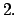
- Si
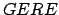 es invertible es invertible
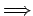 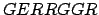 es permitida. es permitida.
- Teorema
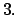
- Teorema
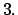 Si Si 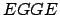 no es invertible no es invertible
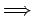 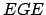 no es permitida. no es permitida.
- Teorema
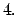
- Teorema
 Si Si 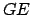 es permitida es permitida
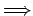 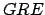 no es invertible. no es invertible.
Ejemplo 5.
Prueba.
-
- 1.
- Note que el Teorema
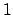 no es una implicación, sin embargo se puede considerar que es una
implicación donde las hipótesis son los 5 axiomas y la conclusión es: no es una implicación, sin embargo se puede considerar que es una
implicación donde las hipótesis son los 5 axiomas y la conclusión es:  es permitida. es permitida.
- 2.
- El Teorema 2 se demostrará utilizando el método directo.
- 3.
- El Teorema 3 se demostrará utilizando el método de contradicción.
- 4.
- El Teorema 4 se demostrará utilizando el método de reducción al absurdo.
Esperamos que al lector le sea de ayuda estas notas.
|

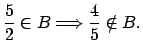
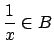 entonces
entonces





