Como primer ejemplo consideremos el clásico Conjunto de Cantor, para su construcción tome el intervalo ![$C_0 = [0,1]$](img31.gif) y divídalo en tres partes iguales.
Al remover el intervalo abierto que corresponde al tercio central, obtenemos
y divídalo en tres partes iguales.
Al remover el intervalo abierto que corresponde al tercio central, obtenemos
![$C_1 = \left[0,\frac13\right] \cup \left[\frac23,1\right]$](img32.gif) . El siguiente conjunto
. El siguiente conjunto 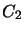 lo
obtenemos removiendo el tercio central a cada intervalo de
lo
obtenemos removiendo el tercio central a cada intervalo de 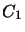 , de manera
que
, de manera
que
![$C_2 = \left[0,\frac19\right] \cup \left[\frac29,\frac13\right] \cup \left[\frac23,\frac79\right] \cup
\left[\frac89,1\right]$](img35.gif) y siguiendo de la misma forma obtenemos una sucesión anidada
de conjuntos cerrados
y siguiendo de la misma forma obtenemos una sucesión anidada
de conjuntos cerrados
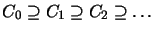 cuyo
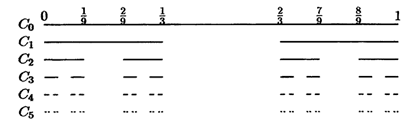
límite llamamos conjunto de los tercios centrales omitidos o Conjunto de Cantor, y lo denotamos por C, Figura 1.
cuyo
límite llamamos conjunto de los tercios centrales omitidos o Conjunto de Cantor, y lo denotamos por C, Figura 1.
Figura:
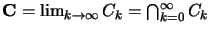
 |
Si consideramos 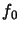 ,
,
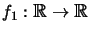 tal que
tal que
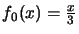 ,
,
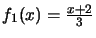 , y con esto definimos un sistema iterado de funciones (IFS) que realizan la lista contractiva de razones
, y con esto definimos un sistema iterado de funciones (IFS) que realizan la lista contractiva de razones
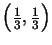 . El atractor de este IFS es el Conjunto de Cantor, [10].
. El atractor de este IFS es el Conjunto de Cantor, [10].
![]() ,
,
![]() tal que
tal que
![]() ,
,
![]() , y con esto definimos un sistema iterado de funciones (IFS) que realizan la lista contractiva de razones
, y con esto definimos un sistema iterado de funciones (IFS) que realizan la lista contractiva de razones
![]() . El atractor de este IFS es el Conjunto de Cantor, [10].
. El atractor de este IFS es el Conjunto de Cantor, [10].