1 2 3 4 5 6 7 8 9 10 11

Comprimiendo y descomprimiendo imágenes con IFS's

Sobre cómo se guarda una imagen en el computador, los diversos métodos de compresión⁴ de imágenes y algunos ejemplos, puede consultar [1], [11]. Pensando en un sentido inverso, acorde con el tema tratado en este artículo, dado un conjunto (figura, foto, etc.), nos podemos preguntar si será posible determinar un sistema iterado de funciones de manera que el atractor de éste sea el conjunto dado? La compresión de imágenes juega un papel importante en el almacenamiento de imágenes con un menor costo, así como en la rápida transmisión de datos. Claro que al comprimir y luego descomprimir estos datos se puede perder información, esta información perdida muchas veces no se percibe por el ojo humano o es redundante, y los métodos de compresión eficientes son los que logran extraer el ``espíritu" de la imagen, para después de descomprimir, reproducir una imagen muy cercana a la original. En la naturaleza muchos objetos mantienen una autosemejanza que se puede representar como el atractor de un sistema iterado de funciones, tal es el caso de las nubes, helechos, plantas, árboles, arbustos, etc. La teoría de los fractales tiene aplicaciones en la compresión de imágenes, en el sentido que podemos pensar que un objeto de esta naturaleza se puede transmitir o guardar eficientemente, reproduciéndolo en el momento que se desee.

El siguiente teorema garantiza que el conjunto invariante puede ser una buena aproximación del conjunto inicial si la unión de copias pequeñas están cerca de éste, pues en este caso tendríamos que $D(E,F)$ se acercaría a cero. En este sentido y como consecuencia de este teorema, el siguiente corolario nos dice que un conjunto compacto se puede aproximar tanto como se quiera, bajo la métrica Hausdorff, por un conjunto autosemejante e invariante de un sistema iterado de funciones. La demostración de ellos se puede encontrar en [6, p. 134]. Si el conjunto es más complicado, este se puede ver como la superposición de varios conjuntos invariantes de varios sistemas de funciones.

Teorema 2 (Collage). Suponga que se tienen $S_i : {\mbox{\conj R}}^n \to {\mbox{\conj R}}^n$funciones de crecimiento acotado $\forall i=1,\dots,m$, y suponga que para todo $i$ se tiene $\vert S_i(x) -S_i(y)\vert\leq c\vert x-y\vert$ para todo $x,y \in {\mbox{\conj R}}^n$, con $c<1$. Sea $E\subset {\mbox{\conj R}}^n$ compacto no vacío, entonces

$$D(E,F)\leq D\left(E,\bigcup_{i=1}^mS_i(E)\right)\frac{1}{1-c}$$ (5)

 

donde $F$ es el conjunto invariante de los $S_i$ y $D$ la métrica Hausdorff.

Corolario 1. Sea $E\subset {\mbox{\conj R}}^n$ compacto no vacío. Para todo $\delta >0$ existe un sistema iterado de funciones de crecimiento acotado $S_1,\dots,S_n$ con conjunto invariante $F$ tal que $D(E,F)<\delta$.

A estas MCRM, se les puede permitir algún estiramiento de la copia, así obtenemos gran variedad de sistemas iterados, con atractores muy variados: Helecho de Barnsley, Figura 9 parte (b); árbol, Figura 10. Estos atractores, a pesar de ser tan naturales, se obtienen de la misma forma que la curva de Koch, el triángulo de Sierpinski, el Twindragon, etc. Sobre estos últimos se dan algunos programas al final, en un lenguaje sencillo, para que el lector interesado pueda experimentar.

Tabla 1: Funciones generadoras.

		$a$	$b$	$c$	$d$	$e$	$f$
Figura	$f_1$	$0.849$	$0.037$	$-0.037$	$0.849$	$0.075$	$0.183$
8	$f_2$	$0.197$	$-0.226$	$0.226$	$0.197$	$0.4$	$0.049$
	$f_3$	$-0.15$	$0.283$	$0.26$	$0.237$	$0.575$	$-0.084$
	$f_4$	$0$	$0$	$0$	$0.16$	$0.5$	$0$
Figura	$f_1$	$0.195$	$-0.488$	$0.344$	$0.443$	$0.4431$	$0.2452$
10	$f_2$	$0.462$	$0.414$	$-0.252$	$0.361$	$0.2511$	$0.5692$
	$f_3$	$-0.058$	$-0.07$	$0.453$	$-0.111$	$0.5976$	$0.0969$
	$f_4$	$-0.035$	$0.07$	$-0.469$	$-0.022$	$0.4884$	$0.5069$
	$f_5$	$-0.637$	$0$	$0$	$0.501$	$0.8562$	$0.2513$

 

Con este esquema de guardar solamente el sistema iterado de funciones y reproducir una aproximación de su atractor en el momento que deseamos, pueden presentarse algunos problemas en cuanto al tiempo de descompresión, aunque la razón de compresión es muy buena, en algunos de estos el tiempo de descompresión no lo es.

Para la descompresión del helecho de Barnsley se usó el sistema de funciones descrito en la Tabla 1. Aplicando este sistema iterado de funciones a $x_0$ obtenemos 4 imágenes, es decir, $\{f_1(x_0),f_2(x_0), f_3(x_0),f_4(x_0)\}$, y al aplicar de nuevo el sistema obtenemos 16 imágenes, así sucesivamente. En este procedimiento el programa que se usó, que se anexa al final del trabajo, representó $4^7$ puntos, pero muchos de ellos están cerca de su imagen, sobre todo los que se obtienen al aplicar $f_4$ y la resolución que se obtiene no es muy buena, Figura 8.

Figura: Helecho de Barnsley aplicando el IFS descrito en Tabla 1.

Figura 9: (a) Juego del Caos. 
(b) Juego del Caos con probabilidades diferentes.

Pensando en este problema, podemos modificar la aplicación del sistema usando el conocido Juego del Caos, en donde en cada paso no aplicamos todas las funciones sino solamente una función de manera aleatoria, todas con la misma probabilidad. Esto quiere decir que si $x_0$ es el punto inicial, tenemos que $x_n=f_{i_{k}}(x_{n-1})$ escogiendo $i_k$ con igual probabilidad del conjunto $\{1,2,3,4\}$. Con este procedimiento se obtuvo la Figura 9 parte (a). Aún así, el Juego del Caos descrito aquí se puede modificar tomando diferentes probabilidades $p_i$ para cada función $f_i$, este proceso recibe el nombre de sistema iterado recurrente de funciones (RIFS); una excelente exposición sobre la existencia, unicidad, convergencia y caracterización del atractor se puede encontrar en [3]. La aplicación a compresión de imágenes lo ilustra John Hart en [8], con algunos ejemplos. Un buen índice, para $\delta$ pequeño, está dado por

$$p_i = \frac{\max(\delta,\vert C_i\vert)}{\displaystyle \sum_{i=1}^n \max(\delta,\vert C_i\vert)},$$ (6)

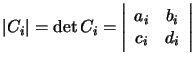donde $\vert C_i\vert= \det{C_i}=\left\vert\begin{array}{cc} a_i&b_i\\ c_i&d_i \end{array}\right\vert$ y se tiene que $\sum p_i = 1$. Con $\delta = 0.01$, con el programa dado al final del trabajo se obtuvo la Figura 9 parte (b), que tiene una mejor resolución con la misma cantidad de puntos que las Figuras 8 y 9 parte (b).

Otros ejemplos de descompresión de un RIFS, aplicado a un punto como imagen inicial, son el árbol de la Figura 10 izquierda, para el sistema de funciones descrito en la Tabla 1 y la rama de la Figura 10 derecha.

Figura 10: Un árbol y una rama como atractores.

Sobre algunos aspectos adicionales a compresión de imágenes, consulte [1], [7], sobre algunos de los métodos de partición de imágenes: Quadtree, partición HV y la partición triangular, [7], [11]. En [7, Apéndice A] se da un programa, en lenguage $C$, para comprimir y descomprimir imágenes usando el esquema HV. Existen además otros esquemas de compresión de imágenes usando la teoría fractal, [7, Caps. 9,13], [9].

1 2 3 4 5 6 7 8 9 10 11