Revista   1 2 3 4  5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31

Programas con opciones

Ya habíamos visto como poner valores default para una variable. Ahora veremos como poner opciones (reglas opts -> val) en un programa

Digamos que nuestro programa se llama prog1 y que tiene varias opciones,los pasos para poner este menú de opciones es como sigue:

1. Hacemos una lista de opciones con su valor default:

Options[prog1]={opcion1-> val1, opcion2->val2,...}

2. En el programa evaluamos la variable opts en las opciones que da el usuario: 

Options[prog1]={opcion1-> val1, opcion2->val2}

prog1[vars_, opts___?OptionsQ]:=Module[{vars locales},

        opt1=opcion1 /. {opts} /. Options[prog1];
        opt2=opcion2 /. {opts} /. Options[prog1];

        (* cuerpo del programa, usa opt1 y opt2 *)

        instr1;
         ...
        instrk                         ];

EJERCICIOS

  1. Investigue los comandos que siguen. Dé ejemplos de su uso.

    StyleForm[],$TextStyle=, StylePrint[], TraditionalForm[], ToString[]

  2. Haga un programa que recibe una expresión algebraica y devuelve los pasos de una posible secuencia de simplificación. Para la salida, use 1.)

  3. Haga un programa que recibe una expresión algebraica y una posible simplificación y devuelve una respuesta: Correcto o Incorrecto + una simplificación correcta si se le pide.

  4. Haga un programa que recibe una lista de ecuación algebraicas y que devuelve algunos pasos de simplificación y la solución. Para este ejercicio use los comandos del ejercicio 1.) para la salida.

  5. Haga un programa que recibe una ecuación algebraica y una posible solución (una lista de valores) y devuelve una respuesta: Correcto o Incorrecto + una solución correcta si se le pide.

  6. Haga un programa que recibe una lista de desigualdades (algebraicas) y, para cada ecuación, devuelve algunos pasos de simplificación y la solución. Para este ejercicio use los comandos del ejercicio 1.) para la salida (ver InequalitySolve[]). Necesitará también este módulo: 

    simbolo[desigualdad_]:=Module[{des,imprima},
                      des=Head[desigualdad];
                      If[des===LessEqual, imprima="<="];
                      If[des===GreaterEqual, imprima=">="];
                      If[des===Less, imprima="<"];
                      If[des===Greater, imprima=">"];
                      imprima
                     ];

  7. Implemente el método de Newton

  8. Repita el ejercicio 2. pero permitiendo que el usuario digite las ecuaciones en lenguaje usual, por ejemplo 2x+1=3x-1 en vez de 2x+1==3x-1. Para esto vea los comandos

    Hold[], HoldPattern[], ReleaseHold[] y SetAttributes[... ,HoldFirst]

    Necesitará hacer algo como: 

    SetAttributes[miprog, HoldFirst];
miprog[var_]=Module[{ec1,ec2,...},
ec1=Hold[var] /. HoldPattern[Set]->Equal;
ec2=ReleaseHold[ec1];
Solve[ec2,x];...
];

  9. Haga animaciones para algunas identidades trigonométricas importantes, verbigracia, cos(x - 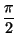$ {\displaystyle {\pi \over 2}}$) = sin(x), sec2x = tan2x + 1, etc.

  10. Haga un programa que recibe una función y hace una animación para traslación vertical y otro para traslación horizontal

  11. Haga un programa que hace una animación del concepto de derivada en un punto

  12. Haga un programa que hace una animación del concepto de integral de Riemann

  13. Haga un programa que hace una animación que ayude a explicar gráficamente,con una animación, que el área entre dos curvas f (x) y g(x), en [a, b] es 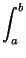$\displaystyle \int_{a}^{b}$| f (x) - g(x)|  dx

  14. Haga un programa que hace una animación del método de los trapecios para aproximar una integral

  15. Haga un programa que haga una animación del Criterio Integral (series) y dé una aproximación de la suma de la serie.

  16. Haga un programa que hace una animación que ilustre el método de exhaución de Arquímides.

  17. Haga un programa que ilustre gráficamente la suma de dos fracciones.

  18. Haga una animación para mostrar el efecto de cambio de base en las gráficas de las funciones exponencial y logarítmica.

  19. Haga un programa que recibe una desigualdad del tipo f (x) 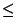$ \leq$ 0 o f (x) > 0 y devuelve un gráfico en el que se indica los intervalos solución de la desigualdad (la gráfica de la función deberá tener colores apropiados)

  20. Haga un programa que ilustre gráficamente las fórmulas notables

Revista   1 2 3 4  5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31

Revista Matemáticas, Educación e Internetâ
Derechos Reservados