Mathematica 

| Walter Mora F. | Revista Digital Matemática, Educación e Internet |
 

Revista   1 2 3 4  5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31

Álgebra elemental y Trigonometría.

$ \bullet$
FACTORIZAR

In[]:= Factor[x^3-y^3] : Out[]= (x - y)(x2 + xy + y2)

$ \bullet$
DESARROLLAR

In[]:= Expand[(x-y)^3] : Out[]= x3 - 3x2y + 3xy2 - y

$ \bullet$
Together[]

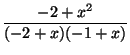In[]:= Together[1/(x-1)+x/(x-2)] : Out[]= $ {\displaystyle {-2 + x^2 \over (-2+x) (-1+x) }}$

$ \bullet$
SIMPLIFICAR

In[]:= Simplify[1/(x-2)+x/(x-2)] : Out[]= $ {\displaystyle {x+1 \over x-2 }}$

$ \bullet$
SIMPLIFICANDO UNA IGUALDAD

In[]:= Simplify[1/(x-2)==-x/(x-2)] : Out[]= $ {\displaystyle {x+1 \over x-2}==0}$

$ \bullet$
COLLECT[...]

In[]:= Collect[x y + a y^2- b y x^2, y] : Out[]= (x - bx2)y + ay2

$ \bullet$
NUMERADOR, DENOMINADOR, COEFICIENTES

In[]:= exp=(x^2+1)/(x^3-x+2);  
Numerator[(x^2+1)/(x^3-x+2)] : x2 + 1
pol=Denominator[(x^2+1)/(4x^3-x+2)] :  4x3 - x + 2
Coefficient[pol,x^3] : 4

$ \bullet$
RESOLVIENDO ECUACIONES Y SISTEMAS

ECUACIONES ALGEBRAICAS

In[]:= N[Solve[ x^2+x-1==0, x]] : Out[]= {{x - > - 1.61803},{x - > 0.618034}}
   
In[]:= Solve[{x^2+y^2==1,x-y==1},{x,y}] : Out[]= {{x - > 0, y - > - 1},{x - > 1, y - > 0}}

ECUACIONES TRIGONOMÉTRICAS

Al intentar resolver una ecuación trigonométrica, MATHEMATICA advierte sobre la posibilidad de no obtener todas las soluciones o la imposibilidad de resolverla en `forma cerrada'.

In[]:= Solve[Cos[x]-Sin[x]==0,x] 

Solve::"ifun":
       "Inverse functions are being used
by Solve, so some solutions may not be found.

Out[]= $ {\displaystyle \{\{x->{-3\pi \over 4} \},\{x->{\pi\over 4}\}\}}$

In[]:= Solve[Cos[x]==x,x] 

Solve::"tdep":
    "The equations appear to involve
     transcendental functions of the variables
     in an essentially non-algebraic way.

Out[]= Solve[Cos[x]==x,x]

En este caso debemos usar algún método numérico para aproximar alguna solución en [0, 2$ \pi$].Como necesitamos una adivinanza inicial, hacemos un gráfico para orientarnos

Plot[Cos[x]-x,{x,-2Pi, 2Pi}]



Ahora, seleccionamos el gráfico (haciendo click sobre él). Presionando Ctrl deslizamos el mouse hasta una posible raíz, obtenemos el valor aproximado de 0.74. Ahora usamos FindRoot[]

In[]:= FindRoot[Cos[x]==x,{x,0.74}]

Out[]= {x - > 0.739085}


EJERCICIOS

Use el Help de MATHEMATICA para investigar los comandos que siguen. Dé Un ejemplo de su uso.

Reduce[],TrigFactor[], TrigReduce[], TrigToExp[], FunctionExpand[], FullSimplify[], ExpToTrig[], TrigToExp[], ComplexExpand[], InequalitySolve[]

Revista   1 2 3 4  5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31

Revista digital Matemática, Educación e Internet.
Derechos Reservados