Punto de Fermat ...

| José Rosales O | Pedro Díaz N.  | Revista Digital Matemática, Educación e Internet |

 

1 2  3  4  5  6  7  8  9  El Teorema de Viviani El teorema de Viviani es un teorema muy elegante que tiene un enunciado sencillo y sorprendente a la vez. (DE VIVIANI) En un triángulo equilátero la suma de las tres distancias de un punto a los lados de un triángulo tiene un valor que es independiente de la posición del punto. Este valor es igual a la altura del triángulo. Para desarrollar la demostración de este teorema es necesario establecer la siguiente convención: Diremos que la distancia de un punto desde un lado de un triángulo a un punto P es considerada como positiva cuando el punto esta dentro del interior del ángulo del triángulo generado por ese lado y algún otro y negativa cuando este afuera En el siguiente dibujo las distancias a los lados son las medidas de los segmentos $\overline{PR}$,$\overline{PS}$,$\overline{PT}$. 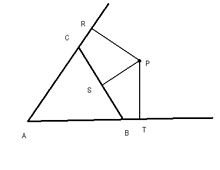De estas medidas solo $\overline{PR}$ y $\overline{PT}$. se consideran positivas en tanto que $\overline{PS}$ es consideradad negativa. Demostración: Considerese un triángulo equilátero $\triangle$PQR. Supóngamos que g es la medidad del lado del triángulo, h su altura y A su área. Es claro que A = $${1\over 2 gh}$$. 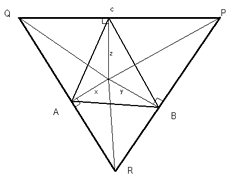Sean x, y, z las distancias de un punto arbitrario O desde los lados $\overline{QR}$,$\overline{RP}$,$\overline{PQ}$ respectivamente y sea S = x + y + z. Considere los triángulos $\triangle$OQR, $\triangle$OPR, $\triangle$OPQ cuyas áreas son A1, A2, A3 respectivamente. Luego A = A1 + A2 + A3 (1) Se tiene que A1 = $${1\over2}$$gx, A2 = $${1\over2}$$gy, A3 = $${1\over2}$$gz pues x, y, x son las alturas sobre $\overline{QR}$,$\overline{RP}$,$\overline{QP}$ de los triángulos $\triangle$OQR,$\triangle$ORP,$\triangle$OPQ respectivamente. Sustituyendo estas igualdades en (1) tenemos $${1\over2} {1\over2} {1\over2}$$ A = (2) $${g\over2}$$ = (3) Pero como A = ${1\over2}$gh entonces ${g\over2}$h = ${g\over2}$(x + y + z). Luego h = s = x + y + z independientemente de la ubicación del punto O.

Revista digital Matemática, Educación e Internet.
Derechos Reservados