|
1 2
3 4
5 6
7 8 9
Sea
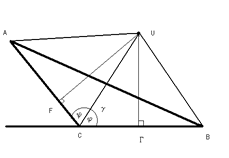
 ABC y sea
n ABC y sea
n ACB = ACB = 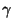 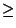 120o. Se debe probar que 120o. Se debe probar que
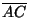 + + 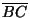 < < 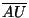 + + 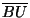 + + 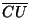 , no importa donde se encuentre U. Considerese además los ángulos , no importa donde se encuentre U. Considerese además los ángulos
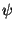 = = 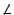 ACU y ACU y
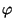 = = 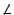 BCU. Tenemos tres casos: BCU. Tenemos tres casos:
- U pertenece al espacio encerrado por el ángulo
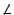 ACB = ACB = 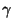 . .
- U pertenece al espacio encerrado por el ángulo adyacente a
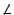 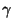 . .
- U pertenece al espacio del ángulo opuesto a
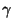
Caso 1. U pertenece al espacio encerrado por el ángulo
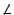 ACB = ACB = 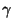 . .
Tenemos que
m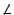 ACU + m ACU + m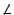 UCB = UCB = 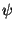 + + 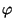 = = 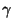 .
Tracense las perpendiculares desde U hasta .
Tracense las perpendiculares desde U hasta
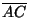 y y
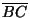 y sean F, G sus intersecciones respectivas. Entonces se tiene que y sean F, G sus intersecciones respectivas. Entonces se tiene que
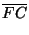 |
= |
x = CU cos(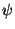 )dondex > 0 )dondex > 0 cos( cos(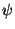 ) > 0 ) > 0 |
|
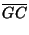 |
= |
y = CU cos(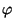 )dondey > 0 )dondey > 0 cos( cos(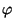 ) > 0 ) > 0 |
|
entonces se tiene que
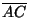 = = 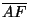 + x y + x y
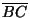 = = 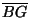 + y y
se obtiene + y y
se obtiene
Ahora bien
| x + y |
= |
CU cos(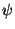 ) + CU cos( ) + CU cos(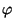 ) = CU(cos( ) = CU(cos(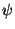 ) + cos( ) + cos(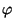 )) )) |
|
| |
= |
2CU cos(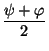 )cos( )cos(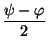 ) ) |
|
| |
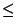 |
2CU cos(60o)cos(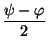 ) ) |
|
| |
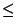 |
CU cos(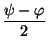 ) ) |
|
| |
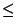 |
CU |
|
Esto indica que
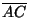 + + 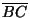 = = 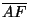 + + 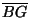 + x + y + x + y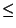 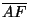 + + 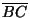 + + 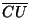 . .
Por último como los catetos
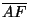 y y
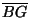 de los triángulos rectángulos de los triángulos rectángulos
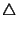 AUF y AUF y
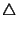 BUG son más pequeños que las hipotenusas BUG son más pequeños que las hipotenusas
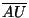 y y
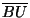 se tiene lo que queriamos probar se tiene lo que queriamos probar
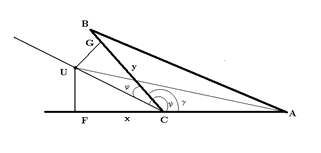
Caso 2.U pertenece al espacio encerrado por el ángulo adyacente a
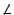 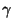 . .
Se supone sin perder generalidad que
m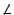 ACU - m ACU - m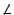 BCU = BCU = 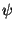 - - 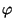 = = 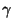 . .
Tracense las perpendiculares desde U hasta
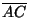 y y
 y sean F,G sus intersecciones respectivas. Entonces y sean F,G sus intersecciones respectivas. Entonces
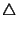 FUC es rectángulo y FUC es rectángulo y
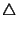 CUG es también rectángulo. Se esto se tiene que CUG es también rectángulo. Se esto se tiene que
Como U pertenece al espacio del ángulo adyacente a
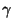 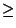 120o entonces
180o 120o entonces
180o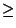 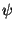 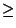 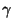 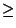 120o 120o 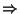 cos( cos(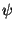 ) < 0. ) < 0.
Por otro lado
180o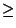 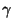 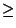 120o 120o 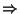 180o 180o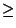 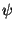 - - 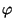 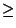 120o 120o 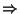 180o + 180o + 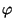 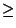 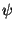 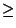 120o + 120o + 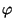 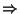 180o 180o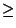 120o + 120o + 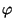 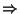 180o - 120o 180o - 120o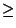 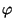 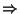 60o 60o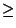 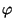 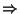 cos( cos(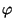 ) > 0 ) > 0 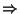 y > 0
Entonces y > 0
Entonces
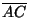 = = 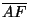 + x y + x y
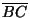 = = 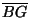 + y de donde + y de donde
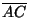 + + 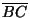 = = 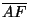 + + 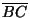 + x + y + x + y
Por otra parte
| x + y |
= |
CU cos(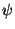 ) + CU cos( ) + CU cos(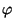 ) = CU(cos( ) = CU(cos(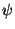 ) + cos( ) + cos(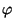 )) )) |
|
| |
= |
2CU cos(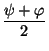 )cos( )cos(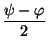 ) ) |
|
| |
= |
2CU cos(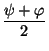 )cos( )cos(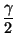 ) ) |
|
| |
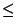 |
2CU cos(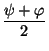 )cos(60o) )cos(60o) |
|
| |
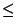 |
CU cos(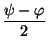 ) ) |
|
| |
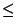 |
CU |
|
|