| |
1 2
3 4
5 6 7
8 9
Con el teorema de Viviani demostrado se puede dar un primer argumento que soluciona el problema que Fermat planteo a Torricelli.
Se necesita establecer primero la siguiente definición
Se llama Punto de Fermat de un triángulo a un punto de este tal que cada lado subtiende un ángulo de 120o con P como vértice.
Un resultado que se deja como ejercicio al lector establece que el punto de Fermat de un triángulo
 ABC es el punto de intersección de los circuncírculos de los tres triángulos equiláteros dibujados exteriormente sobre los lados del triángulo ABC es el punto de intersección de los circuncírculos de los tres triángulos equiláteros dibujados exteriormente sobre los lados del triángulo
 ABC ABC
Seguidamente mostramos un primer resultado del problema planteado.
El punto de triángulo dado
 ABC tal que la suma de las distancias a los vértices del triángulo es mínima, es el punto P de Fermat del triángulo siempre que el triángulo ABC tal que la suma de las distancias a los vértices del triángulo es mínima, es el punto P de Fermat del triángulo siempre que el triángulo
 ABC no tenga ángulos mayores de 120o. ABC no tenga ángulos mayores de 120o.
Sea
 ABC un triángulo y supongamos que no tiene ángulos mayores de 120o. Localícese el punto P de Fermat. Sean
t1 = ABC un triángulo y supongamos que no tiene ángulos mayores de 120o. Localícese el punto P de Fermat. Sean
t1 = 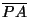 , t2 = , t2 = 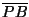 , t3 = , t3 = 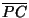 en A, B, C respectivamente. Entonces podemos afirmar que el triángulo en A, B, C respectivamente. Entonces podemos afirmar que el triángulo
 xyz formado por las perpendiculares xyz formado por las perpendiculares
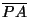 , ,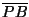 , ,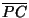 es un triángulo equilátero. Para probar este resultado basta ver que los ángulos internos de es un triángulo equilátero. Para probar este resultado basta ver que los ángulos internos de
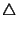 xyz miden 60o. Sin perdida de generalidad lo haremos para el ángulo xyz miden 60o. Sin perdida de generalidad lo haremos para el ángulo 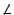 x. Sea x la intersección de la perpendicular x. Sea x la intersección de la perpendicular
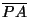 con la perpendicular con la perpendicular
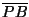 . Considere el cuadrilátero . Considere el cuadrilátero
XAPB entonces
m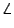 x + m x + m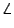 A + m A + m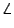 P + m P + m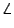 B = 360o B = 360o
|
(4) |
De la definición del punto P se tiene que
m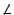 P = 120o. Además
m P = 120o. Además
m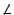 B = m B = m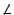 A = 90o por construcción. Luego sustituyendo en (4) de tiene A = 90o por construcción. Luego sustituyendo en (4) de tiene
m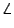 x x + 90 o + 120 o + 90 o = 360 o 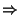 m m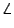 x x + 300 o = 360 o 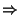 m m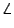 x x = 60 o
De donde se tiene que el triángulo es equilátero.
Entonces por el teorema de Viviani se tiene que
donde h es la altura del triángulo
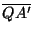 Sea Q Sea Q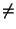 P y sean P y sean
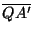 , ,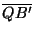 , ,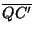 las perpendiculares a los lados del triángulo las perpendiculares a los lados del triángulo
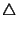 xyz. Se tiene que
Q xyz. Se tiene que
Q 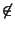 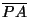 , Q , Q 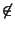 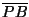 , Q , Q 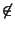 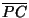 . Sea
QA' = c1, QB' = c2, QC' = c3,. Sean además
i1 = . Sea
QA' = c1, QB' = c2, QC' = c3,. Sean además
i1 = 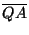 , i2 = , i2 = 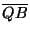 , i3 = , i3 = 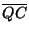 las distancias de Q a los vértices del las distancias de Q a los vértices del
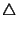 ABC. Considere sin pérdida de generalidad el triángulo ABC. Considere sin pérdida de generalidad el triángulo
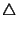 QAA'. Entonces por construcción se tiene que QAA'. Entonces por construcción se tiene que
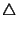 QAA' es rectángulo en A' de donde QAA' es rectángulo en A' de donde
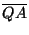 > > 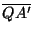 . Pero esto dice que . Pero esto dice que
i1 > c1;i2 > c2;i3 > c3
de donde, por el teorema de Viviani
i1 + i2 + i3 > c1 + c2 + c3 = h
Lo que dice que P es el punto que minimiza la distancia tal y como queriamos demostrar.
Finalmente, si Q = P el resultado es evidente.
El caso en el cual el triángulo
 ABC posee un ángulo de medida mayor o igual a 120o es un tanto más elaborado ABC posee un ángulo de medida mayor o igual a 120o es un tanto más elaborado
Considere un triángulo
 ABC que posee un ángulo cuya medida es mayor a 120o. Entonces el punto P donde la suma de las distancias a los vértices es mínima es igual al vértice del a´ngulo mayor. ABC que posee un ángulo cuya medida es mayor a 120o. Entonces el punto P donde la suma de las distancias a los vértices es mínima es igual al vértice del a´ngulo mayor.
|

