El Problema de Fermat para Torricelli.

1 2 3 4 5 6 7 8 9

Entonces $\overline{AC}$ + $\overline{BC}$ = $\overline{AF}$ + $\overline{BC}$ + x + y $\le$ $\overline{AF}$ + $\overline{BC}$ + $\overline{CU}$ y como los catetos $\overline{AF}$ y $\overline{BG}$ de los triángulos rectángulos $\triangle$ AUF y $\triangle$ BUG son más pequeños que las hipotenusas $\overline{AU}$ y $\overline{BU}$ se tiene la desigualdad buscada

$\displaystyle \overline{AC}$ + $\displaystyle \overline{BC}$ < $\displaystyle \overline{AU}$ + $\displaystyle \overline{BU}$ + $\displaystyle \overline{CU}$

Caso 3. U pertenece al espacio del ángulo opuesto a $\gamma$

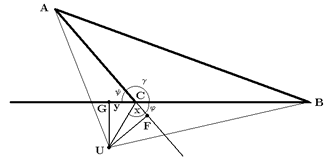
En este caso tenemos que $\psi$ + $\varphi$ = 360 - $\gamma$ . Sean F y G los puntos de las bases de las perpendiculares trazadas desde U sobre $\overline{AC}$ y $\overline{BC}$ respectivamente. Se tienen dos subcasos:

180^o < $\gamma$ + $\psi$ $\le$ 270^o
270^o < $\gamma$ + $\psi$ $\le$ 360^o - $\varphi$

Subcaso 1. 180^o < $\gamma$ + $\psi$ $\le$ 270^o

Sea $\alpha$ = $\angle$ GCU y $\beta$ = $\angle$ UCF $\Rightarrow$ $\alpha$ = $\psi$ + $\gamma$ - 180 de donde se tiene que

cos( $\displaystyle \alpha$ ) = - cos( $\displaystyle \psi$ + $\displaystyle \varphi$ )

Pero $\psi$ + $\varphi$ = 360^o - varphithen $\psi$ + $\gamma$ = 360^o - $\varphi$ $\Rightarrow$ cos( $\alpha$ ) = - cos( $\varphi$ ) de donde

y = - $\displaystyle \overline{CU}$ cos( $\displaystyle \varphi$ )

Análogamente,

$\beta$ = $\varphi$ - m $\angle$ BCF pero como $\angle$ BCF $\equiv$ $\angle$ ACG = $\psi$ - $\alpha$ $\Rightarrow$ $\beta$ = $\varphi$ - ( $\psi$ - $\alpha$ ) = $\varphi$ - ( $\psi$ - ( $\psi$ + $\gamma$ - 180^o)) = $\varphi$ + $\gamma$ - 180^o $\Rightarrow$ cos( $\beta$ ) = cos( $\varphi$ + $\gamma$ - 180^o) = cos( $\varphi$ + $\psi$ )cos(180^o) - sen $\nolimits$ ( $\varphi$ + $\psi$ )sen $\nolimits$ (180^o) = - cos( $\varphi$ + $\varphi$ ) = - cos( $\varphi$ + (360 - $\psi$ - $\varphi$ ) = - cos(360 - $\psi$ ) $\Rightarrow$ cos( $\beta$ ) = - cos( $\psi$ ). Asi

x = - $\displaystyle \overline{CU}$ cos( $\displaystyle \psi$ )

Luego tenemos que

$\displaystyle \overline{AC}$	=	$\displaystyle \overline{AF}$ + x
$\displaystyle \overline{BC}$	=	$\displaystyle \overline{BG}$ + y

Ahora bien

x + y	=	- $\displaystyle \overline{CU}$ cos( $\displaystyle \psi$ ) + - $\displaystyle \overline{CU}$ cos( $\displaystyle \varphi$ ) = - $\displaystyle \overline{CU}$ (cos( $\displaystyle \psi$ ) + cos( $\displaystyle \varphi$ ))
	=	-2 $\displaystyle \overline{CU}$ cos $\displaystyle \big($ $\displaystyle {\psi+\varphi\over 2}$ $\displaystyle \big)$ cos $\displaystyle \big($ $\displaystyle {\psi-\varphi\over 2}$ $\displaystyle \big)$
	=	-2 $\displaystyle \overline{CU}$ cos $\displaystyle \big($ $\displaystyle {360^\circ\gamma\over 2}$ $\displaystyle \big)$ cos $\displaystyle \big($ $\displaystyle {\psi-\varphi\over 2}$ $\displaystyle \big)$
	=	-2 $\displaystyle \overline{CU}$ cos $\displaystyle \big($ 180^o - $\displaystyle {\gamma\over 2}$ $\displaystyle \big)$ cos $\displaystyle \big($ $\displaystyle {\psi-\varphi\over 2}$ $\displaystyle \big)$
	=	-2 $\displaystyle \overline{CU}$ $\displaystyle \Big[$ cos(180^o)cos( $\displaystyle {\gamma\over 2}$ ) + sen $\displaystyle \nolimits$ (180^o)sen $\displaystyle \nolimits$ ( $\displaystyle {\gamma\over 2}$ ) $\displaystyle \Big]$ cos $\displaystyle \big($ $\displaystyle {\psi-\varphi\over 2}$ $\displaystyle \big)$
	=	-2 $\displaystyle \overline{CU}$ (- cos( $\displaystyle {\gamma\over 2}$ ))cos $\displaystyle \big($ $\displaystyle {\psi-\varphi\over 2}$ $\displaystyle \big)$
	=	2 $\displaystyle \overline{CU}$ cos( $\displaystyle {\gamma\over 2}$ )cos $\displaystyle \big($ $\displaystyle {\psi-\varphi\over 2}$ $\displaystyle \big)$

Como acordamos que $\gamma$ $\ge$ 120^o $\Rightarrow$ ${\gamma\over 2}$ $\ge$ 60^o $\Rightarrow$ cos( ${\gamma\over 2}$ ) $\le$ 60^o. Luego

x + y	=	2 $\displaystyle \overline{CU}$ cos(60^o)cos $\displaystyle \big($ $\displaystyle {\psi-\varphi\over 2}$ $\displaystyle \big)$
	$\displaystyle \le$	$\displaystyle \overline{CU}$ cos $\displaystyle \big($ $\displaystyle {\psi-\varphi\over 2}$ $\displaystyle \big)$
	$\displaystyle \le$	$\displaystyle \overline{CU}$

De donde obtenemos

$\displaystyle \overline{AC}$ + $\displaystyle \overline{BC}$ $\displaystyle \le$ $\displaystyle \overline{AF}$ + $\displaystyle \overline{BC}$ + $\displaystyle \overline{CU}$

De nuevo, como los catetos $\overline{AF}$ y $\overline{BG}$ de los triángulos rectángulos $\triangle$ AUF y $\triangle$ BUG son más pequeños que las hipotenusas $\overline{AU}$ y $\overline{BU}$ se tiene que

$\displaystyle \overline{AC}$ + $\displaystyle \overline{BC}$ $\displaystyle \le$ $\displaystyle \overline{AU}$ + $\displaystyle \overline{BU}$ + $\displaystyle \overline{CU}$

tal i como queriamos probar.

El Subcaso 2. es análogo y se deja como ejercicio al lector.

Existen otras demostraciones sobre el punto de Fermat. En 1929 J.F Hoffman reaizo una demostración para en caso cuando el triángulo tiene un ángulo mayor de 120^o sin embargo su demostración no fue considerada original hasta que el matemático Tibor Galai demostro la independencia de la demostración.

Por otra parte, Jacob Steiner realizo otra demostración utilizando circulos y elipses en su argumento y el matemático Daniel Pedoe realizo una demostración basada en los tres excículos del triágulo.