
|

|
Una demostración FísicaUn argumento muy elegante sobre la existencia del punto de Fermat es uno que utiliza un argumento de tipo físico basado en un procedimiento de Arquímedes.
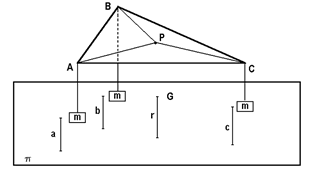
Consideremos un triángulo
Desde un punto P en el triangulo son pasados hilos sobre las poleas y una masa m es suspendida al final de cada hilo. Se libera el sistema y se deja a la aación de la fuerza de gravedad.
La posición tomada por el punto P es el punto de Fermat del
DemostraciónEn la posición de equilibrio las masas m tendrán alturas a, b, c arriba del plano horizontal
Sea G el centroide del sistema y sea r su distancia sobre
en virtud del principio de composición de fuerzas de Galileo. Luego,
donde se alcanza el mínimo potencial de energía. Se sabe que una condición necesaria y suficiente para que un punto sometido a varias fuerzas este en equilibrio es que las resultantes de las fuerzas aplicadas a el sea nula. Esto equivale a decir que la suma geométrica de ellas es un polígono cerrado.
Entonces G se encuentra más cercano a
Sea h la distancia desde el triángulo
(h - a) + (h - b) + (h - c) = 3h - (a + b + c)
Si t es el tamaño total del hilo y S es la medida de los segmentos horizontales entonces
S = t - [3h - (a + b + c)] = (t - 3h) + (a + b + c)
y como t y h son constantes y (a + b + c) es mínima se encuentra en la posición de equilibrio.
Por otro lado, el punto de Fermat cumple las siguientes especificaciones:
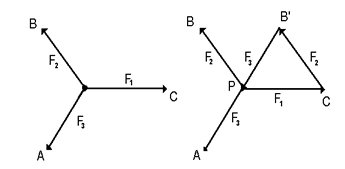
Como
Considere el triángulo
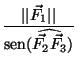 = = 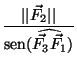 = = 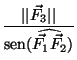
Luego, como
||
sen
Y como la suma de los tres ángulos es 360o se tiene que cada ángulo mide 120o.
Esto prueba que P es el punto de Fermat.
|
Revista digital Matemática, Educación e Internet.
Derechos Reservados