1 2
3 4
5 6
7 8
9 10
La teoría de números transfinitos se ha desarrollado aún más allá de los números cardinales. Después de la construcción de los números cardinales se establece la construcción de los cardinales inaccesibles. Se dice que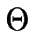 
es un cardinal inaccesible "si no puede ser alcanzado por medio de la suma de 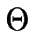ordinales menores que 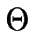'' (Ortiz, 1994).
La teoría de números transfinitos no puede establecer la existencia de estos números inaccesibles dentro de la axiomática de Zermelo-Fraenkel y debe recurrir a una generalización de esta introduciendo un ``axioma de infinitud generalizado'' llamado el axioma de inaccesibilidad que indica que
"existe al menos un cardinal inaccesible'' (Shoenfield,1967).
``Existe toda una teoría de cardinales grandes, entre los cuales encontramos: cardinales indescriptibles, inefables, Ramsey, Mahlo, fuertemente compactos, supercompactos y, finalmente los cardinales extensibles. Estos últimos son los cardinales más grandes que se consideran actualmente en la Teoría de Conjuntos'' (Ortiz,1994).
1 2
3 4
5 6
7 8
9 10
Revista digital Matemática, Educación e Internet.
Derechos Reservados
