|
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
1.1.1.
Ecuaciones separables. La ecuación
(3) es una ecuación en variables separables si
f(x,y) se puede escribir en la forma
f(x,y) = g(x)h(x)
, En este caso, (3) equivale a
, o bien,
. En esta ecuación las variables aparecen separadas, lo cual permite integrar
ambos lados de la misma para obtener
.
De
igual manera, la ecuación (5) es
una ecuación en variables separables si es
posible escribir
M
y
N
en la forma
M(x,y)=g1(x)h1(y)
y
N(x,y)=g2(x)h2(y)
. Si este es el caso, la ecuación (5) se escribe en la forma
, en la cual las variables aparecen separadas, lo cual permite integrar ambos
miembros y obtener la solución en cuadraturas.
1.1.2.
Ecuaciones exactas. Supongamos que la
ecuación
define implícitamente
una función diferenciable
en algún intervalo. Si derivamos
ambos lados de la ecuación
con respecto a
x
resulta
, que se puede escribir en la forma (5) con
y
, de manera que la ecuación diferencial
tiene por solución la función
definida por la ecuación
.
Recíprocamente,
supongamos que se da la ecuación diferencial
(5). Si existe una función
tal que
y
(6)
de
modo que la ecuación
defina implícitamente
una función diferenciable
en algún intervalo, entonces
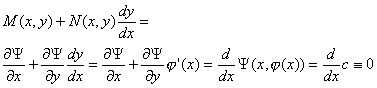
En este caso, se dice que la ecuación (5) es una ecuación diferencial exacta. El siguiente teorema nos proporciona un criterio de exactitud.
Teorema
1. Sean las funciones
M
, N
,
y
continuas en la región rectangular
R:
,
. Entonces la ecuación (5) ,
es exacta en R si, y sólo si,
(7)
Si la ecuación
(5) es exacta, entonces es posible obtener su solución en cuadraturas en la
forma
. En efecto, de (6) se sigue que
, luego si se integra esta ecuación con respecto a
x
se obtiene :
(8)
La función
h
es una función arbitraria de
y
que hace las veces de la constante
arbitraria. Además, siempre es posible escoger
h
de modo que
. En efecto, Derivando ambos lados
de (8) con respecto a
y
resulta :
(9)
Pero, de (6),
, luego si se sustituye esta expresión en (9), entonces al despejar
nos queda:
(10)
Para determinar h(y) de (10) es esencial que, independientemente de su apariencia, el miembro del lado derecho de la ecuación (10) sea sólo función de y , para lo cual basta demostrar que su derivada con respecto a x es idénticamente igual a cero. En efecto, de acuerdo a la ecuación (7),
.
De esta manera, para obtener h(y) se integra la expresión del lado derecho de (10) con respecto a y (sin sumar la constante arbitraria de integración). Al conocer h(y) , de la ecuación (10) se obtiene la primera integral de la ecuación (5) en la forma
siendo c una constante arbitraria.